ПОНЯТИЯ И МЕТОДЫ МАТЕМАТИЧЕСКОЙ ТЕОРИИ ПЕДАГОГИЧЕСКИХ ИЗМЕРЕНИЙ

(ITEM RESPONSE THEORY, IRT)

Статья третья

Вадим Аванесов

testolog@mail.ru

Аннотация

В первой[1] и во второй[2] статьях рассматривались понятия и модели математической теории педагогических измерений МТИ (IRT). В третьей статье продолжается анализ основных понятий и начинается изложение методов этой теории.

Метод в науке вовсе не есть дело личного вкуса или какого-нибудь внешнего удобства…, а есть, сверх своих формальных значений, само развитие содержания, - эмбриологии истины, если хотите.

Герцен А.И.

Простые истины МТИ

МТИ начинается с очень простой истины: при ответе на задание теста испытуемые с лучшей подготовкой имеют больше шансов на успех, чем испытуемые с худшей подготовкой. Это можно представить в форме графика, представленного на рис.1. Все остальные понятия, аксиомы, формулы, методы и результаты МТИ основаны на этой истине и на трёх основных функциях, по которым могут строиться графики реальных заданий.

Важно подчеркнуть, что в настоящем тесте каждое задание имеет свой уникальный графический образ. Образ одного задания отличается от другого задания значениями хотя бы одного, по меньшей мере, из трёх формальных параметров функции, по значениям которых строятся графики заданий. Сущность параметров заданий уже освещалась в двух предыдущих статьях.

Рис.1. График вероятности правильного ответа на задание теста.

Графики строятся по итогам эмпирической апробации каждого задания проектируемого теста на достаточно представительной выборке испытуемых. Когда возникает вопрос о минимально необходимом числе испытуемых, отвечать приходиться примерно так: применяя статистические методы, мы пытаемся по выборочным характеристикам (статистикам) оценить значение параметров в генеральной совокупности. При этом значения параметра считаются тем точнее, чем больше объём выборочной совокупности.

Можно ли выразить графически вероятность решения не тестовых заданий, а например, задач? Абстрактно говоря, можно. Если провести эмпирическую апробацию интересующих задач и получить матрицу результатов их решения на множестве испытуемых. Тогда можно получить графики зависимости вероятности их правильного решения от уровня подготовленности испытуемых. Но метод графического изображения отмеченной вероятности принято делать только для тестовых заданий. Что связано с тем, что расчёт параметров заданий выполняется в рамках разработки тестов как средства педагогических измерений, как содержательной и формальной системы заданий возрастающей трудности. В другие рамки графический метод не вписывался пока что должным образом.

Педагогическое измерение было определено как процесс определения меры интересующего свойства личности испытуемого на латентной интервальной шкале посредством качественного теста, состоящего из системы заданий равномерно возрастающей трудности, позволяющего получать педагогически целесообразные результаты, отвечающие критериям надёжности, валидности, объективности и эффективности. В этом определении курсивом выделены основные термины, позволяющие отграничить признаки педагогических измерений, от прочих методов, научных и не научных[3].

Главное интересующее свойство личности, измеряемое в процессе педагогических измерений - это уровень подготовленности испытуемых, которое рассматривается как латентное свойство. В определение этого свойства включаются знание учебной дисциплины, умения, навыки, представления и компетенции. Свойство - это внешне выражение непосредственно не наблюдаемого, латентного качества личности. Всё перечисленное образует уровень подготовленности.

В теории педагогических заданий[4] были выделены содержательные и формальные требования к тестовым заданиям, а также было показано, что тестовые задания должны отвечать не только содержательным, но и формальным требованиям[5], подтверждаемых эмпирически. А потому к первой простой истине можно добавить вторую простую истину, часто игнорируемую в российской практике: без эмпирической проверки формальных свойств настоящих тестовых заданий не бывает.

Ранее утверждалось, что задания, не прошедшие эмпирическую проверку, в лучшем случае могут быть лишь заданиями в тестовой форме[6]. В худшем случае - это вопросы или задачи, не пригодные для применения в тесте. Вопросы и задачи с неизвестными мерами трудности, коррелируемости и прочими формальными показателями в настоящий тест не включаются.

Не всякая практика - критерий истины

Хотя всякая истина должна подтверждаться на практике, соотношение простой идеи и существующей практики, как говорят любители псевдонаучного тумана, неоднозначно. Даже если практика показывает, что простая идея не подтверждается, дело не в идее – с ней всё в порядке. Ошибочными могут оказаться предварительные оценки уровня подготовленности испытуемых, само задание, либо своеобразная практика проверки знаний, допускающая списывание, подсказки, а то и масштабные подтасовки, которых раньше в системе образования не было.

В МТИ чем круче выглядит график, тем точнее, на меньшем диапазоне, задание различает испытуемых по уровню их подготовленности. В этой логике идеалом могли бы стать задания, отвечающие требованиям шкалы Л.Гутмана. В ней испытуемые, отвечающие правильно на трудные задания, непременно должны отвечать правильно и на предыдущие лёгкие задания[7]. Но в практике такая схема не выдерживается из-за отсутствия требуемого числа идеальных заданий и испытуемых с идеальной структурой знаний. Практика порождает как случаи ординарные, похожие на рис.1, так и случаи, когда хуже подготовленные испытуемые отвечают на задание лучше, чем хорошо подготовленные. Казалось бы, парадокс.

Так бывает, когда задание плохо сформулировано; хорошо подготовленные испытуемые понимают его не так, как другие, а потому ошибаются чаще остальных. Такой график указывает на нарушение первой простой истины, и, следовательно, на некачественность задания. В практике разработки тестов ординарные случаи встречаются примерно в сто раз чаще неординарных.

Американская служба тестирования (ETS) в прежние годы коллекционировала графики неординарных заданий. Интересно было выяснить причины, почему появляются такие странные графики заданий? У автора этой статьи есть свой ответ: потому что эти задания - не тестовые. Что случается чаще всего из-за логических ошибок, допущенных при их формулировке. Методы МТИ и статистической теории измерений (СТИ) выявляют такие некачественные задания на стадии предварительной эмпирической проверки и исключают, тем самым, возможность ошибочного включения подобных заданий в тест.

В СТИ для выявления неординарных заданий чаще других используется метод расчёта коэффициентов корреляции ответов испытуемых на задание с суммой баллов, полученной по ответам по всему проектируемому тесту. В МТИ используется другой метод - расчёт значений критерия хи-квадрат. Кроме того, в настоящем тестировании проверяется надёжность и валидность исходных результатов, проверяется тестобразующие свойства всех, до единого, тестовых заданий и устанавливается эффективный общественный контроль в процессе тестирования.

Только в таком случае возникают черты Национального тестирования, имеющего место в США, Казахстане и других странах, где обязательны два главных компонента – признанный профессионализм тестологов и общественная экспертиза полученных результатов. В России нет ни того, ни другого, потому что в такого рода «помехах» не заинтересованы чиновники. В результате вместо методов педагогических измерений мы получили ЕГЭ, разработкой и проведением которого руководят они сами[8].

Идеальных тестовых заданий не бывает

Это можно считать третьей истиной МТИ, которая нередко опровергается практиками. Они показывают графики замечательно работающих в тесте заданий. Учебники и задачники тоже содержат некоторую часть хороших и отличных заданий для обучения. Но для тестирования эти задания могут оказаться не подходящими.

Вообще между задания для обучения и тестовыми заданиями существует асимметричное соотношение. Не все, а только очень малая часть заданий для обучения имеют шанс стать тестовыми заданиями. Но все тестовые задания могут успешно применяться и для контроля, и для обучения.

В силу разных причин в российском образовании оказалось слишком много заданий не технологичных и не пригодных для применения в тестах. Да и отношение к тестам в педагогической среде весьма противоречивое, если не сказать, часто отрицательное.

В системе образования каждый учитель работает так, как он знает и как может. Использование иного метода, может быть и хорошего, но не знакомого или недостаточно освоенного, обычно приносит только вред. Отсюда проистекает педагогический консерватизм, который надо преодолевать целенаправленным повышением педагогической квалификации по вопросам педагогических измерений. Для заданий, которые кажутся очень близкими к идеалу, в МТИ применяется англ. термин overfit, что можно перевести примерно так: эти задания настолько хороши (для теста), что в это трудно поверить.

Естественно выяснить вопрос - почему не бывает, или почти не бывает, идеальных тестовых заданий?

Во-первых, содержание задания должно точно соответствовать цели тестирования и содержанию учебного процесса; не содержать в себе факторы, выходящие за пределы содержания учебного курса. В реальности главными критериями конкурсного отбора абитуриентов, например, по математике, являются знания формул, умение их применять, умение решать типовые задания и задачи, хорошая память и практические навыки их решения за короткое время. Хотя в идеале выдвигаются иные требования: счётно-аналитические умения абитуриентов, уровень логического мышления и творческие способности[9]

Во-вторых, надо иметь задание, абсолютно понятное всем испытуемым. Но это трудно достигнуть из-за затруднений гностического характера у испытуемых. Каждый понимает текст задания по-своему. Хорошо, если большинство понимает так, как задумал автор задания. Почти каждое впервые предлагаемое разработчиком задание нуждается в минимизации словесного состава и в повышении смысла используемых слов.

В-третьих, надо подобрать форму задания, наиболее подходящую для содержания. Опыт автора показывает, что для этого требуется специальное обучение разработчика заданий. Формы тестовых заданий технологичны, но имеют ряд недостатков. Один из недостатков – возможность угадать правильный ответ.

В идеальном случае тестирования хорошо бы позволить испытуемым отвечать на задание в той форме, в которой они умеют это делать лучше. У кого хорошо развита речь, тому легче отвечать устно. Другие тяготеют к письменной форме проверки. Третьих привлекает тестовая форма, четвёртые лучше понимают текстовые задания, пятые, напротив, лучше понимают только формульные и символьные записи. Но в реальном тестировании такое разнообразие форм невозможно; там технология, а потому все испытуемые вынуждены проходить испытания в заданной технологией форме.

В заданиях с выбором одного или нескольких правильных ответов идеальным можно было бы назвать такое задание, где доля выбора каждого дистрактора[10] была бы одинаковой. Но в реальности, при разработке теста, дистракторный анализ показывает, что предлагаемые ответы в каждом задании неодинаково привлекательны для испытуемых. Некоторые из дистракторов выбираются чаще, другие реже. Есть и такие предлагаемые на выбор ответы, которые вообще не выбираются испытуемыми. В таком случае, ответы не имеют свойства дистракторов, они подлежат удалению из заданий проектируемого теста.

Вместо удаляемых дистракторов приходится искать другие. В настоящий тест задания с невыбираемыми или с редко выбираемыми дистракторами (менее 5 %) не включаются. Подбор примерно равно привлекательных дистракторов для каждого тестового задания – это задача для специально обученного педагога-методиста экстра-класса.

Практически методы МТИ нацелены на поиск заданий не идеальных, а просто подходящих для разработки теста, как системы заданий равномерно возрастающей трудности, позволяющей качественно и эффективно измерить уровень подготовленности испытуемых.

Две основные теории педагогических измерений

МТИ – это не только теория, но и совокупность методов обоснования качества каждого отдельного задания проектируемого теста, и теста в целом. Не случайно одна из точных характеристик МТИ – это теория, ориентированная на исследование каждого задания теста; в отличие от СТИ, ориентированной, главным образом, на анализ свойств теста в целом[11].

В таких случаях правильнее говорить о научном подходе к созданию систем измерения. Слово «научном» здесь не лишнее. Потому что системы измерения, как показывает практика, могут быть не только научные, но и не научные, псевдонаучные и даже антинаучные. Короче, МТИ – это больше, чем теория. Это система измерения, объединяющая теорию и методы.

Каждая наука представляет собой единство теории и метода. Это единство скрепляется методологией, которая по определению занимается развитием теории и творческим преобразованием практики. При этом велика роль понятийного аппарата.

Система понятий педагогических измерений исследовалась в обеих статьях автора по IRT[12], опубликованных в журнале ПИ. Все понятия были разделены по принципу принадлежности к той или иной теории. Там же упоминалась идея неточности и метафоричности английского названия МТИ - Item Response Theory (IRT). От статьи к статье часть понятий развивалась и переопределялась, появлялись новые термины. Например, вместо «характеристических кривых» появился термин «график задания». Потребность в замене возникла в процессе углубления в смыслы используемых понятий. В науке переосмысление понятий – неизбежный процесс.

Редко бывает, чтобы в рамках одной науки существовала только одна теория или только один метод. Чем больше развита наука, тем больше в ней создаётся условий для возникновения новых и конкурирующих теорий, по-разному объясняющих интересующий нас мир. Различающимися оказываются и методы, основанные на различных теориях.

В более чем столетней истории[13] научного развития педагогических измерениях наиболее зримо и эффективно проявляют себя две основные теории.

Статистическая (классическая) теория педагогических и психологических измерений появилась, по времени, первой. Удивительно, но это была одна общая теория нескольких наук, имевших название Behavioral, что в переводе на русский язык «поведенческие» звучит не очень понятно.

Между тем, этим названием основатели хотели, по-видимому, показать, что для выживания человечества важно всесторонне изучить человека и научиться изменять его поведение в лучшую сторону, что невозможно сделать без психологических, социологических, педагогических измерений. Уместно вспомнить выражение классика русской педагогики К.Д. Ушинского: если педагогика хочет воспитывать человека во всех отношениях, то она должна прежде узнать его тоже во всех отношениях»[14].

Прикладной наукой для психологии стала психометрика (psychometrika), для социологии – социометрия, для педагогики – педагогические измерения (educational measurements). Названные науки оказались несравнимо больше развиты за рубежом, нежели в России. С годами отставание в развитии этих наук не уменьшается, а увеличивается.

Ключевые понятия (категории, критерии) статистической теории педагогических измерений – это тест, задания, мера трудности, корреляция, критерии надёжности и валидности. К этому набору автор этой статьи добавил ещё два критерия – объективность[15] и эффективность[16] тестовых результатов.

            Математическая теория измерений (МТИ, Item Response Theory, IRT) появилась как следствие развития статистической теории. Вначале это была общая теория педагогических психологических и социологических измерений (IRT), в фокусе которой ставился не столько тест, сколько отдельное задание или каждый вопрос социологической анкеты. Это важная особенность IRT дала возможность углубленного и дифференцированного анализа каждого задания теста, статистический аппарат для выявления менее подходящих заданий, с целью их замены на более подходящие.

Математическая теория педагогических измерений опирается не только на статистику, но и на теорию вероятности и её методы. Различие в сути наук. Статистика - наука индуктивная, связана с движением мысли от частного к общему, а теория вероятностей - наука дедуктивная, а потому ход мысли при её применении, от общего – к частному. Все модели МТИ основаны на теории вероятности, а практика её применения для оценки качества педагогических заданий и теста в целом основана на статистических доказательствах.

Уточнение понятий МТИ

В первой статье рассматривались такие понятия, как параметры уровня подготовленности испытуемого (θ_i) и уровня трудности задания β_j . Среди других ключевых понятий МТИ - функция, называемая часто математической моделью педагогического измерения, графики трёх основных функций[17], или по-старому, моделей педагогических измерений. Рассматривались также понятия «латентная переменная величина», «различающая способность задания»[18] и другие.

В МТИ уровень подготовленности испытуемых рассматривается как переменная величина, принимающая, теоретически, значения от минус бесконечности до плюс бесконечности. Практически, в нормальной тестовой практике, пределы варьирования значений уровня подготовленности 99,99 % испытуемых обычно оказываются в пределах значений -5 < θ_i < +5, где i может принимать значения с 1 до N, N – число испытуемых.

Такую переменную величину можно представить умозрительно. Её можно пытаться воспроизвести по итогам проверки подготовленности посредством системы гомогенных заданий и сложения баллов за правильные ответы на каждое задание. Получаемую при этом переменную величину на Западе стали называть реально видимой (manifest variable), содержащей тестовые баллы испытуемых и ошибки измерения.

Подлинный смысл измерения заключается в поисках истинных значений уровня подготовленности испытуемых на переменной величине, и эти значения предстоит определить. Величину, содержащей истинные значения, F.M.Lord в 1952 году назвал латентной[19]. Получаемые при тестировании баллы испытуемых являются эмпирическими проявлениями не видимой, явно, латентной переменной величины[20]. Справедливости ради надо отметить, что понятие «латентная переменная величина» было введено раньше в социологических измерениях известным учёным P. Lazarsfeld[21].

Метод построения графических образов заданий

по эмпирическим данным[22]

Этот метод использовался в старой психометрике. Истоки его применения обнаруживаются в трудах А. Бине и Т. Симона[23], а затем и Марион Ричардсон[24]. Для оценки качества заданий они делили всех испытуемых на группы, в зависимости от полученного тестового балла. Далее строили точки на плоскости, соответствующие доле правильных ответов на интересующее задание в каждой уровневой группе испытуемых.

При построении графика каждого задания желательно, чтобы число испытуемых было более тысячи; при этом условии появляется возможность разделить их на так называемые балльные группы, с достаточным числом в каждой из групп. В рамках данного метода, на первом этапе создаются отдельные группы тех, кто имеет ноль баллов (если таковые будут), один, два, три и т.д. Соответственно, такие группы испытуемых иногда называют группами нулевиков, единичников, двоечников, троечников, четверочников, пятерочников, шестёрочников и т.д. На оси абсцисс откладывают баллы, дающие название каждой группы.

Затем в каждой такой балльной группе подсчитывается доля правильных ответов. Значение этой доли в каждой балльной группе и откладывается на оси ординат. В итоге на плоскости откладываются точки, соединение которых даёт ломаную линию, похожую на рис. 2.

Тестовые баллы (X)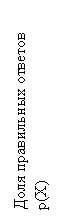

	Рис.2. Общая тенденция роста доли правильных ответов на задание, в зависимости от тестовых результатов в балльных группах испытуемых.

Каждое задание теста имеет свой специфический график, потому что каждое имеет свою меру трудности, свой уровень дифференцирующей способности на определенном интервале оси подготовленности[25]. Для случая построения графика по эмпирическим баллам эту ось обозначим символом Х[26].

Трудно найти задания с одинаковым потенциалом измерения. На рис. 3 представлен графический образ неудачного задания. График этого задания имеет малую крутизну, что означает довольно низкую дифференцирующую способность. Чем выше крутизна графика, тем лучше работает задание на интервале измерения. Но в случае с заданием на рис.3 наблюдается противоположная картина; интервал измерения для него – вся шкала, от нуля до 20 баллов. На каждом балльном уровне оно «работает» с дефектом, плохо различия знающих от незнающих.

Можно задать уточняющий вопрос: а почему задание на рис. 3 отнесено к числу неудачных? Потому что, во-первых, оно сравнительно легкое для самых незнающих; 30% слабо подготовленных испытуемых справляются с ним. Напомним, что на оси Х отложены значения тестовых баллов испытуемых, а на оси ординат – доли правильных ответов (p), полученных в каждой балльной группе испытуемых. Произведение (р · 100) и даёт отмеченный процент. Во-вторых, оно оказывается довольно трудным для части хорошо подготовленных испытуемых.

Столь противоречивая сущность данного задания выражается и на графике. Там обращает на себя внимание слабый, а можно сказать и чуть эмоциональнее, вялый прирост доли (или процента) правильных ответов, в зависимости от уровня подготовленности испытуемых. Дифференцирующая способность оказалась низкой на всех значениях континуума измерения. И даже в группе самых подготовленных испытуемых доля правильных ответов не превышает 65 процентов.

Рис. 3. Графический образ задания, плохо дифференцирующего испытуемых любого уровня подготовленности.

Тестовые баллы (X)

Педагогическая интерпретация таких заданий примерно такова. Это задание с тремя ответами. Вероятность угадывания правильного ответа в нём не менее 33%. Задание плохо сформулировано, поэтому о правильном ответе приходится только догадываться. На нём ошибаются и слабые, и хорошо подготовленные испытуемые. Следовательно, высока и погрешность измерения. Вот почему такому заданию в тесте места нет. Хотя оно может быть в тестовой форме, оно не тестовое по существу.

Задание требует переработки в направлении достижения большей ясности его смысла испытуемыми всех уровней подготовленности. Тогда его станут лучше понимать и соответственно, лучше решать. В первую очередь те, кто лучше подготовлен. Здесь самое время ещё раз затронуть мысль о соотношении понимания и знания. Задания нужно формулировать так, чтобы их смысл был понятен всем испытуемым. Если кто-то не понимает, то виноват разработчик задания, а не испытуемый. Давно сказано - кто ясно мыслит, тот ясно излагает (Шопенгауэр).

Построение образов по эмпирическим данным имеет преимущества в смысле реалистичности и наглядности изучаемых тестовых свойств заданий в конкретной совокупности испытуемых.

Второй метод построения графических образов заданий основан на математических моделях педагогического измерения. При использовании таких моделей получаются гладкие функции, параметры которых позволяют точнее характеризовать потенциальные возможности каждого задания. Зная параметры, можно моделировать тест с интересующим уровнем трудности, и с так называемым уровнем информативности, что связано с понятием адекватности теста реальному уровню подготовленности испытуемых. Методы построения гладких графиков на основе математических функций рассматривались ранее.[27]

Редактирование матриц исходных результатов испытуемых[28]

Самый первый метод, предваряющий создание теста в соответствии с любой теорией педагогических измерений - это построение матриц тестовых результатов и их редактирование. Все матрицы тестовых результатов полезно делить на две группы – редактированные и не редактированные. Для разработки педагогических тестов используются только редактированные матрицы данных. Эти матрицы публикуются в научных отчётах, что обеспечивает  возможность проверки качества создаваемого теста. Самый верный способ похоронить надежду на создание качественных тестов - это скрывать матрицы исходных тестовых баллов.

Матрица представляет в обобщённом виде результаты всех испытуемых, на все задания. Краткий пример различий между матрицами можно видеть при сравнении табл. 1 и 2. В табл.1 сверху, снизу, слева и справа матрицы расположены номера испытуемых, номера заданий и суммы баллов – всё это выделено курсивом Они являются элементами не матрицы, а таблицы.

Табл. 1 Пример матрицы исходных результатов проектируемого теста

Задания
Исп.	1	2	3	4	5	6	7	Сумма
1	1	1	1	1	1	1	1	7
2	1	1	1	1	1	1	0	6
3	1	1	1	1	1	0	0	5
4	1	1	1	1	0	0	0	4
5	1	1	1	0	0	0	0	3
6	1	1	1	0	0	0	0	3
7	1	1	1	0	0	0	0	3
8	1	1	1	0	0	0	0	3
9	1	1	0	0		0	0	2
10	1	0	0	0	0	0	0	1
Cумма	10	9	8	4	3	2	1	33

Педагогическое измерение требует обязательного редактирования исходных матриц результатов проектируемого теста[29]. В этой работе тестологи опираются на два понятия. Первое из них - экстремальные задания. В приведённой для примера матрице табл. 1 экстремальным является задание №1. На него правильно ответили все испытуемые. Оно оказалось очень лёгким, в процессе апробации никого не дифференцировало по уровню подготовленности, а потому оказалось непригодным для применения в тесте. Экстремальным (непригодным) называется также и задание, на которое ни один испытуемый не может дать правильный ответ. Оно также удаляется из матрицы исходных результатов, поскольку тоже никого не дифференцирует, но по причине завышенной трудности. В табл. 1 такого задания нет.

Второе понятие - экстремальные испытуемые. В табл. 1 к таковым относится первый испытуемый. Он ответил на все задания, и это означает, что его уровень подготовленности выше уровня трудности проектируемого теста. Надо либо добавлять в тест более трудное задание, либо удалять такого испытуемого из матрицы, как оказавшегося несоответствующим уровню трудности заданий. Уровень его подготовленности предлагаемой системой заданий точно измерить невозможно.

После удаления экстремальных испытуемых и заданий получается редуцированная матрица. В ней номера заданий и испытуемых можно поменять, но можно и оставить, во избежание путаницы, до момента практического применения теста. Редуцированная матрица представлена в табл. 2

Табл. 2 Пример редуцированной матрицы.

Исп.	2	3	4	5	6	Сумма
2	1	1	1	0	1	5
3	1	1	1	1	0	4
4	1	1	1	0	0	3
5	1	1	0	0	0	2
6	1	1	0	0	0	2
7	1	1	0	0	0	2
8	1	1	0	0	0	2
9	1	0	0		0	2
10	0	0	0	0	0	0
Cумма	9	8	4	3	2	33

После удаления экстремальных заданий может возникнуть новое экстремальное задание. Здесь это стали №№ 2 и 7. Могут также появиться новые экстремальные испытуемые. Здесь это №№ 8 и 10. Их тоже удаляют. Остаются элементы табл. 3.

Табл. 3. Вторая редуцированная матрица.

Исп.	3	4	5	6	Сумма
2	1	1	0	1	3
3	1	1	1	0	3
4	1	1	0	0	2
5	1	1	0	0	2
6	1	0	1	0	2
7	0	1	0	0	1
8	1	0	0	0	1
Cумма	6	5	2	1	14

Для прекращения эффекта возникновения новых экстремальных заданий и испытуемых в результате удаления строк и столбцов матрицы, иногда искусственно добавляются вектор-столбец или вектор-строка, профиль которых прекращает отмеченный эффект.

Методы определения параметров тестовых заданий

и параметров испытуемых

Понятие «трудность задания» является не абсолютным, а относительным. В статистической теории педагогических измерений трудность задания определяется как статистическая мера его не решаемости испытуемыми данного множества. Это статистическая доля неправильных ответов. Относительность этой меры зависит преимущественно от состава группы испытуемых. Чем лучше подготовлены испытуемые, тем легче оказывается задание.

В МТИ чем больше тестируемая группа, тем точнее и устойчивее получаемый параметр трудности задания. Определение данного параметра проводится в два этапа. На первом этапе рассчитываются примерные эмпирические значения параметра трудности задания, обозначаемые латинской буквой b_j, где j – номер задания. Эта примерные значения меры трудности заданий представлены в последней строке учебной матрицы табл. 4, нередко приводимой в статьях автора из соображений обеспечить доступность и наглядность излагаемого материала. Они являются лишь начальными оценками истинных значений параметров трудности заданий. Параметрами трудности заданий они могут стать после уточнения методом максимального правдоподобия и процесса шкалирования значений логарифмических мер трудности заданий.

Пример таблицы исходных тестовых результатов               Табл.4.

№№	Х1	Х2	Х3	Х4	Х5	Х6	Х7	Х8	Х9	Х10	Yi	pi	qi	pi/qi	lnpi/qi
1.	1	1	1	0	1	1	1	1	1	1	9	.90	.10	9	2.20
2.	1	1	0	1	1	1	1	1	1	0	8	.80	.20	4	1.39
3.	1	1	1	1	0	1	1	0	1	0	7	.70	.30	2.33	.85
4.	1	1	1	1	0	1	0	1	0	0	6	.60	.40	1.50	.40
5.	1	1	1	1	1	1	0	0	0	0	6	.60	.40	1.50	.40
6.	1	1	1	1	0	0	1	0	0	0	5	.50	.50	1.00	0
7.	1	1	0	1	1	0	1	0	0	0	5	.50	.50	1.00	0
8.	1	1	1	1	1	0	0	0	0	0	5	.50	.50	1.00	0
9.	1	0	1	0	1	1	0	0	0	0	4	.40	.60	.66	-.42
10.	0	1	1	0	0	0	0	1	0	1	4	.40	.60	.66	-.42
11.	1	1	1	0	0	0	0	0	0	0	3	.30	.70	.43	-.84
12.	1	1	0	0	0	0	0	0	0	0	2	.20	.80	.25	-1.39
13.	1	0	0	0	0	0	0	0	0	0	1	.10	.90	.11	-2.21
Rj	12	11	9	7	6	6	5	4	3	2	65
Wj	1	2	4	6	7	7	8	9	10	11
pj	.923	.846	.692	.538	.462	.462	.385	.308	.231	.154	5
qj	.077	.154	.308	.462	.538	.538	.615	.692	.769	.846
pjqj	.071	.130	.213	.248	.248	.248	.236	.213	.178	.130
qj/pj	.083	.182	.445	.859	1.164	1.164	1.597	2.246	3.329	5.493
lnqj/pj	-2.489	-1.704	-.810	-.152	.152	.152	.468	.809	1.202	1.703

Только после этого появляются основания говорить о педагогическом измерении уровня трудности заданий[30].

Чем труднее задание, тем правее располагается его график. Точнее, проекция точки перегиба функции более трудного задания на ось абсцисс располагается правее. Этим объясняется второе английское название параметра трудности задания – location parameter. В компьютерных программах для разработки тестов по МТИ для характеристики меры трудности заданий чаще используется второе название.

Метод вычисления параметра крутизны заданий

На значение, а значит, и на расположение меры трудности задания в МТИ оказывает некоторое влияние параметр крутизны заданий. Чем выше значение параметра крутизны (а_j) задания теста, тем левее, при прочих равных условиях, на графике оказывается точка перегиба функции задания.

Напомним, что параметр крутизны (а_j) задания под номером j является частью всех трёх моделей педагогических измерений. В однопараметрической модели Г. Раша значение этого параметра принимается равным единице, что делает крутизну всех заданий теста одинаковой. Вследствие чего этот параметр в формуле 1 не приводится.

P_j {x_ij = 1½β_j}= exp(q - β_j) / (1 + exp(q - β_j)                                                (1)

При пользовании двухпараметрической моделью МТИ параметр a_j является важной частью формулы, а потому возникает вопрос вычисления значения этого параметра для каждого задания.

P_j{ = 1½b_j, a_j}= exp a_j(q - b_j)/(1 + exp a_j(q - b_j)                                      (2

Процесс вычисления a_j облегчается тем, что F.М.Lord обнаружил связь между значениями коэффициентов корреляции ответов на задания теста с суммой баллов испытуемых и значениями a_j. Эта связь выражается формулой 3, где символ ρ_j выражает идею меры связи ответов испытуемых на задание под номером j c суммой баллов,

a_j =                                                                                   (3)

Поскольку значения ρ_j, коэффициентов корреляции в генеральной совокупности испытуемых реально неизвестны, вместо них нередко в качестве оценки интересующей меры связи используется один из бисериальных коэффициентов корреляции, или классический коэффициент корреляции Пирсона. Матрица коэффициентов корреляции Пирсона между всеми заданиями табл. 4 и суммой баллов представлена в табл. 5 [31].

Табл. 5.    КОРРЕЛЯЦИОННАЯ МАТРИЦА

	1	2	3	4	5	6	7	8	9	10	ryj
1	1,000	-,1231	-,192	,3118	,2673	,2673	,2282	-,4330	,1581	-,6770	0,132
2	-,1231	1,0000	,178	,4606	-,0329	-,0329	,3371	,2843	,2335	,1818	0, 488
3	-,1920	,178	1,0000	,051	-0,051	,283	-,0158	,083	-0,030	,284	0, 305
4	,3118	,4606	0,051	1,0000	,2381	,2381	,4148	-,0514	,1409	-,4606	0,495
5	,2673	-,0329	-,051	,2381	1,0000	,3810	,2196	,0514	,2254	,0329	0,495
6	,2673	-,0329	0,283	,2381	,3810	1,0000	,2196	,3858	,5916	,0329	0,707
7	,2282	,3371	-0,158	,4148	,2196	,2196	1,0000	,1581	,6928	,1011	0,652
8	-,4330	,2843	,083	-,0514	,0514	,3858	,1581	1,0000	,4260	,6396	0,534
9	,1581	,2335	-,030	,0141	,2254	,5916	,6928	,4260	1,0000	,2725	0,752
10	-,6770	,1818	,284	-,4606	,0329	,0329	,1011	,6396	,2725	1,0000	0,293

Последовательный расчет значений параметров крутизны заданий для данных табл. 4 по формуле 3 представлен в табл. 6.

Табл. 6. Пример расчёта значений параметра а_j  для данных табл. 5 .

№ № заданий	rjy	rjy2	1 - rjy2	rjy2	aj
1	0, 132	0.017	0,983	0,991	0,133
2	0,488	0.238	0,762	0,873	0,559
3	0,305	0.093	0,907	0,952	0,320
4	0,495	0.244	0,756	0.869	0,570
5	0,495	0.244	0,756	0,869	0,570
6	0,707	0.498	0,502	0,708	0,999
7	0,652	0.424	0,576	0,759	0,859
8	0,534	0.285	0,715	0,845	0,632
9	0,752	0.565	0,435	0,659	1,140
10	0,293	0.086	0,914	0,956	0,306

При сопоставлении значений второго и последнего столбцов можно заметить связь: чем выше значения коэффициентов корреляции, тем больше значения параметра а_j.

Противоречивые смыслы и разрушительная роль третьего параметра

Третий параметр оценки качества тестового задания с_j. часто называют параметром угадывания, но это надо признать спорным. F.M. Lord в своих ранних работах обращал внимание на то, что во время тестирования не все испытуемые пытаются угадывать ответ, а только те, кто не знает правильный ответ. А потому угадываемость правильного ответа зависит не только от формы и содержания задания, но и от уровня подготовленности испытуемых. Отсюда и уточнённое им название - параметр псевдоугадывания.

Формальный смысл этого параметра – это мера зависимости правильного ответа на задание из-за вероятности угадывания правильного ответа. Иными словами, вероятность правильного ответа на задание, с выбором одного правильного ответа нередко завышается из-за возможности угадывания.

Ф. Бейкер полагает, что добавление третьего параметра с_j  в формулу вероятности правильного ответа приводит к утере математических свойств логистической функции. Из-за этого он считает, что трёхпараметрическую модель уже нельзя считать логистической функцией[32].

                         (4)

Надо заметить, что добавление третьего параметра вводит диссонанс в содержательную интерпретацию получаемой вероятности правильного ответа. Из формулы 4 видно, что значение с_j принимается одинаковым для испытуемых, любого уровня подготовленности. Но это – элемент эрозии первой простой истины и упрощение реальной тестовой ситуации: хорошо подготовленные испытуемые не угадывают ответы, а решают задания и находят правильные ответы.

Слабо подготовленные испытуемые ведут себя противоположным образом. Решение заданий они заменяют угадыванием правильного ответа. Тестирование для них превращается в лотерею или в игру «угадайку». То и другое далёко от идеалов качественной образовательной деятельности. Таким образом, можно определённо утверждать, что содержательная интерпретация параметра с_j   входит в противоречие с формальной интерпретацией.

В отмеченном противоречии можно усмотреть одну из причин, по которым многие исследователи не склонны применять в своей работе трёхпараметрическую формулу для определения вероятности правильного ответа испытуемых на задания теста. В этом смысле самую радикальную позицию занимал Г.Раш. Он отвергал не только трёхпараметрическую функцию определения вероятности правильного ответа, но и двухпараметрическую. Идея теста как системы заданий возрастающей трудности не сочетается с возможностью пересечений графиков различных заданий[33] из-за различий в значениях параметра крутизны заданий.

У параметра с_j обнаруживается ещё один весомый дефект. В однопараметрической и двухпараметрической функциях заданий нижним пределом вероятности правильного ответа у очень слабо подготовленных испытуемых является ноль. Соответственно, параметр трудности задания определялся как проекция точки перегиба функции на ось абсцисс, т.е. латентный уровень подготовленности испытуемых. Ведение в функцию третьего параметра сдвигает вверх, как уже отмечалось, нижний предел значений вероятности правильного ответа. Мера сдвига вычисляется по формуле P (θ) = c + (1 – c) (0,5).

После раскрытия скобок и перестановки членов получаем, что вероятность правильного ответа на задание среднего уровня трудности повышается до уровня

P (θ) =  1/2 (1+c).

Этот эффект фактического облегчения заданий наглядно представлен на примере рис. 2. Там мы имели дело с возможностью угадывания 0, 25 при ответе на задание среднего уровня трудности. При с_j = 0,25 вероятность правильного ответа на задание средней трудности становится  P (θ) =  1/2 (1+ 0,25) = 0, 625. Именно это значение и отложено на оси ординат рис. 4.

Рис. 4. График задания, представленный в соответствии с трёхпараметрической моделью оценки вероятности правильного ответа испытуемых.

Игнорирование роли параметра с_j разрушительно повлияло на качество результатов ЕГЭ. Именно высокая вероятность угадывания правильных ответов на задания части «А» стала первой причиной некачественности КИМов ЕГЭ. Если 25-30 баллов по некоторым КИМам являются двойкой в привычном для школы содержательно-ориентированном истолковании результатов ЕГЭ, то это значит, что угадывание, подсказки и помощь там стало главным фактором обесценивания левой части шкалы результатов КИМов[34].

Очевидно, такие результаты не являются педагогическими измерениями. Большое количество (порядка 30-ти) баллов в КИМах у абсолютных двоечников – слишком наглядный признак демаркации теста как метода педагогических измерений от псевдоизмерений посредством КИМов ЕГЭ[35]. набрать в тесте такое количество баллов неподготовленному испытуемому невозможно.

Параметр псевдоугадывания с_j влияет на трудность задания. С увеличением значения с_j возможностей для угадывания правильного ответа возрастают, а потому график функции становится заметно пологим. В результате задание становится, в среднем, легче.

С увеличением значений c_j  у слабо подготовленных испытуемых повышается вероятность правильно ответить на задание и получить незаслуженные ими баллы. График задания становится пологим.

Методы статистической обработка результатов в МТИ[36]

Первые методы статистической обработки данных возникли в статистической теории педагогических измерений. В рамках статистической теории главные методы обоснования качества педагогических измерений – статистические расчёты показателей средней тенденции, показателей вариации, расчёт коэффициентов корреляции, множественный регрессионный и факторный анализ, методы расчёта надёжности и валидности тестовых результатов. Основные положения статистической теории педагогических и психологических измерений рассматривались в публикациях нашего журнала.

Формулы и примеры таких расчётов приведены в ранее опубликованной статье[37], поэтому здесь они не приводятся.

Существуют и более продвинутые методы статистической обработки результатов при разработке теста. К их числу можно отнести множественный регрессионный и факторный анализ. Регрессионный анализ позволяет определить вклад каждого задания в общую вариацию значений тестовых баллов, а факторный анализ – определить меру гомогенности создаваемого теста.

Расчёт вероятностей правильных ответов – ключевой метод МТИ

Расчёт вероятностей правильного ответа испытуемых разного уровня подготовленности на задания разного уровня трудности можно назвать ключевым методом МТИ. Эти расчёты приводятся на основе одно, двух- и трёхпараметрических моделей измерений. Примеры вычисления вероятностей правильных ответов в зависимости от уровня подготовленности испытуемых, по двух- и трёхпараметрическим моделям читатель уже приводились в первой статье автора по IRT[38].

Ниже даётся пример метода вычисления вероятностей правильного ответа испытуемых различного уровня подготовленности на задание теста по однопараметрической модели, в которой вероятность правильного ответа вычисляется по формуле

 P_j (q) = .                                                                                     (1)

Для упрощения расчётов, значения параметров а_j и b_j в данном примере примем равными 1.

Вначале находится вероятность правильного ответа для испытуемого очень низкого уровня подготовленности испытуемого, со значением q_I= -3,0.

Первый шаг: рассчитывается разность параметров L = (q - b_j ). Подставляя эти данные, получаем L = (-3,0 – 1,0) = -4,0.  Далее e^-L  = 2, 71828^-(-4,0)  = 54,59801.

Второй шаг. Находится значение знаменателя формулы (1):

1+ 54, 59801 = 55,59801.

Третий шаг: Находится вероятность правильного ответа. P_j (q) = =  = 0,018315.

Интерпретация полученного результата. Для испытуемых очень низкого уровня подготовленности, равного –3,0 логита, вероятность правильного ответа на задание уровня трудности 1,0 логит равна 0,018315. Что вполне согласуется с первой истиной: в нормально организованном процессе тестирования правильный ответ малоподготовленного испытуемого на трудное задание весьма маловероятен.

Теперь пришло время посмотреть – как меняется вероятность правильного ответа на одно и то же задание для испытуемых, имеющих сравнительно высокий уровень подготовленности. Для этого достаточно провести небольшой вычислительный эксперимент, в котором можно последовательно брать разные уровни подготовленности (с мелким шагом, чтобы график был гладким). Здесь взят шаг +1) и свести полученные данные в таблицу 4.

Таблица 4 результатов вычислительного эксперимента по определению вероятности правильного ответа испытуемых различного уровня подготовленности на задание с параметрами трудности b = 1,0.

Уровень подготовленности  испытуемых , qi	L =j(q - bj )	e –L	1 + e –L	Pj (q)
-3,0	(-3-1) = -4	54,59	55,598	0,018
-2,0	(-2-1)=-3	20,08	21,086	0,047
-1,0	(-1-1)= -2	7, 389	8,389	0,166
0	(0-1)= -1,0	2, 718	3, 716	0,269
1.0	(1-1) = 0	1	2	0,500
2.0	(2-1)= 1,0	0,368	1,368	0,731
3.0	(3-1)= 2	0,135	1,135	0,881

По значениям табл. 4 можно построить график вероятности правильных ответов испытуемых на интересующее задание, в зависимости от уровня подготовленности. Чем мельче шаг значений первой колонки, тем более гладкой становится искомая функция. Алгоритмы вычислений вероятности правильного ответа по другим моделям представлены в ранее опубликованной статье[39].

Пример метода вычисления истинных тестовых баллов испытуемых

В МТИ вычисляется истинный тестовый балл испытуемого на латентной переменной величине, представляющей интересующее свойство личности на непрерывной линии (континууме), от самых низких, до самых высоких значений. Методы вычисления этой величины в каждой теории заметно различаются.

Формула расчёта истинного тестового балла испытуемого (True Score), по версии D.N.Lawely, вводилась в предыдущей работе[40]. Этот балл обозначается символом TS_i и вычисляется как сумма вероятностей правильных ответов испытуемого[41].

                        TS_i = ,

В данной статье даётся порядок вычислений значений TS_i. Применение этой формулы для расчёта истинного тестового балла испытуемого показано на доступном примере очень короткого «теста», состоящего всего из четырёх заданий[42]. Напомним, что настоящий тест всегда содержит большее число заданий. После того, как определены меры трудности и значений коэффициентов крутизны заданий теста, находятся значения вероятности правильного ответа испытуемого интересующего уровня подготовленности на имеющиеся задания теста.

Возьмём случай расчета истинного тестового балла испытуемого (θ = 1.0). 2-х-параметрическая модель. «Тест» состоит из 4 заданий. У этих заданий ранее были определены следующие значения параметров:

 b₁ =-1.0   b₂ =0,75  b₃ =0     b₄ =0,5

 а₁ =0.5    a₂ =1.2    a₃ =0,8  a₄ =1.0

Считаются вероятности правильного ответа на все четыре задания «теста».

P₁ (1.0) = 1/(1 + EXP (-.5(1.0 - (-1.0)))) = .73

P₂ (1.0) = 1/(1 + exp(-1.2 (1.0- (.75)))) = .57

P₃ (1.0) = 1/(1 + EXP (-.8 (1.0 -(0)))) = .69

P₄ (1.0) = 1/(1 + EXP(-1.0 (1.0 - (.5)))) = .62

Складываются полученные значения вероятностей:

ТSi =0,73 + 0,57 + 0,69 +0, 62 = 2,61

Это и есть истинный тестовый балл испытуемого, полученный в данном коротком «тесте».

Интерпретация графических образов заданий

В процессе эмпирического обоснования метрических свойств каждого задания проектируемого теста ему ставится в соответствие график изменения вероятности  правильного ответа испытуемых в зависимости от уровня подготовленности испытуемых. В литературе на английском языке эти графики названы item characteristic curves. На русском языке эти графики получили название «характеристические кривые заданий», что звучит непонятно. Автор этой статьи в последнее время стал использовать другое, более простое понятие - график задания.

Уже отмечалось, что каждое задание теста имеет свой специфический график, потому что каждое имеет свою меру трудности, свой уровень различающей способности на определенном интервале оси подготовленности[43]. Трудно найти задания с одинаковым потенциалом измерения. И уже совсем редко находятся задания, которые имеют минимум погрешностей измерения.

График задания можно истолковать как нелинейную регрессию, где независимой переменной является уровень подготовленности испытуемых θ, а зависимой переменной величиной - вероятность правильного ответа испытуемых на задание теста.

На рис. 6. представлены два графика заданий одинаковой трудности, но с различающимися значениями параметра a_j. Это случай, который называют вторым парадоксом Ф.Лорда. Первый парадокс Ф.Лорда касался вопросов соотношения надёжности и валидности тестовых результатов. Он заметил, что после определённого порога чем выше была надёжность тестовых результатов, тем ниже оказывалась их валидность. Второй парадокс Лорда - интерпретационный. Оказалось, что некоторые задания ведут себя парадоксально: они оказываются то лёгкими, то трудными в группах испытуемых с низким и высоким уровнем подготовленности.

Рис. 6. Иллюстрация второго парадокса Ф.Лорда[44].

Эти два задания неодинаковы по трудности для испытуемых разного уровня подготовленности. Второе задание оказалось легче для слабо подготовленных, но труднее для хорошо подготовленных испытуемых. Оно имеет невысокую различающую способность и у слабых, и у хорошо подготовленных испытуемых. Его из проектируемого теста лучше удалить. А в тест него надо включить первое задание, имеющее более высокую дифференцирующую способность среди хорошо подготовленных испытуемых.

При интерпретации графиков заданий Ф. Бейкер считает необходимым помнить следующее[45]:

1. Если уровень различающей способности задания (a_j) меньше среднего, то график задания похож на пологую прямую линию. Оно слабо дифференцирует испытуемых.

2. Если уровень различающей способности задания выше среднего, то график задания похож на S – образную линию, и он довольно крутой в своей средней части.

3. Если уровень трудности задания меньше среднего, то вероятность правильного ответа у большинства испытуемых больше, чем 0,5. Если уровень трудности задания выше среднего, то вероятность правильного ответа у большинства испытуемых меньше, чем 0,5.

4. Задания располагаются на оси абсцисс в соответствии с уровнем их трудности, независимо от их уровня различающей  способности задания. Это факт подтверждает независимость этих двух характеристик.

5. При нулевой различающей способности задания трудность задания принимается равной 0,5. Потому что для таких заданий мера трудности не определяется.

6. Точка Р (θ) =0,5 соответствует уровню трудности задания.

Другие методы МТИ

В рамках одной статьи нет возможности рассмотреть всё множество методов МТИ. В последующих публикациях подлежат рассмотрению методы проведения дистракторного анализа посредством графиков МТИ, анализ эффективности тестовых заданий и теста посредством расчёта информационных функция, применение статистических методов в МТИ для оценки меры пригодности заданий и меры совместимости заданий в тесте.

Отдельного внимания заслуживают методы МТИ в адаптивном обучении и контроле. Эти методы применяются также выравнивания и сравнения тестовых результатов в зависимости от уровня трудности тестовых заданий и теста, для поиска смещённых (biased) заданий, неодинаково работающих в разных группах испытуемых, для разработки теста, моделирования тестов, для анализа эффективности математических методов оценки параметров испытуемых и заданий.

Есть ещё один круг методов МТИ можно назвать прикладным. Это применение методов МТИ для диагностики болезней и сравнительной эффективности лекарств, для сравнительной оценки качества образования и уровня жизни населения различных территорий и стран. В прикладных работах почти всегда наблюдаются попытки подмены проблематики педагогических измерений и языка педагогических измерений проблемами и языком техники, математики, медицины и т.п. Это существенное основание, по которым ряд авторов не могут публиковать у нас свои работы по МТИ, вполне хорошие для соответствующих отраслей, но не отвечающие задаче развития педагогических измерений.

Особое внимание привлекает проблематика Rasch Measurement (RM). Некоторые авторы рассматривают её как часть общей математической теории педагогических измерений, в то время как другие авторы исходят из идеи несводимости измерительной системы Rasch Measurement к МТИ, подчёркивают её оригинальность. В 2010 году редакция планирует публикацию ряда статей по данной системе.