ОСНОВНЫЕ ПОНЯТИЯ И ПОЛОЖЕНИЯ  

МАТЕМАТИЧЕСКОЙ ТЕОРИИ ИЗМЕРЕНИЙ

(ITEM RESPONSE THEORY)

Статья вторая

Вадим Аванесов

testolog@mail.ru

Аннотация

В первой статье[1] название Item Response Theory (IRT) было переведено на русский язык как «математическая теория педагогических измерений». Но эта теория применяется не только в педагогических, но широко используется также в психологических, социологических, медицинских измерениях. Для того, чтобы снять возникшую неточность, во второй статье  название было поправлено. Оно потеряло неспецифическое слово «педагогических» и, таким образом, стало короче на одно слово.  Теперь IRT лучше переводить на русский язык как  математическую теорию измерений (МТИ). 

Во второй статье исследуются истоки МТИ, углублены и расширены ранее сформулированные понятия, а также представлены определения других основных понятий МТИ (IRT).

Спорный научный статус МТИ (IRT)

Уже отмечалось, что на русском языке IRT  (МТИ) часто характеризуется как  «современная» теория педагогических измерений. Этим допускается сразу три ошибки.

Во-первых, другие теории как бы автоматически переводятся в разряд несовременных, что, конечно же, порождает множество ошибок и отрицательных последствий, в теории и в практике.  Ни одна подлинно научная теория не исчерпывает себя до конца; она развивается, трансформируется и действует в рамках принятых условий и ограничений.

Во-вторых, IRT - теория вовсе не педагогическая, а математико-статистическая. Терминология IRT, язык и научный аппарат совершенно точно не входит  в состав педагогической науки. Известные зарубежные авторы R.K.Hambleton & R.W.Jones[2], E.H.Haertal[3], W.M.Yen[4] и многие другие, если не все,  также считают IRT не педагогической теорией. Они называют её  математической или статистической теорией.  И действительно, IRT опирается на язык математики, статистики, в ней широко представлены знания по теории вероятностей, математической статистики и вычислительных методов математики. Всё это, вместе взятое, относится к прикладной математике и к математической статистике, и применяется в ряде других наук.  В современных науках немало таких теорий, и они используются для формального обоснования качества педагогических, психологических, социологических и прочих измерений. Учитывая общность языка математики, теории вероятности и математической статистики, а также факт широкого применения IRT в общественных науках, в данной статье в качестве основного названия на русском языке в этой статье принято новое название IRT -  «математическая теория  измерений (МТИ)».

И наконец, третья ошибка заключается в том, что современными считаются[5] не одна, а три основных теории, применяемые сейчас в педагогических и психологических измерениях: это статистическая (классическая) теория, МТИ (IRT) и расширенная статистическая теория (РСТ). Последняя по-английски называется Generalizability Theory (G-Theory) [6].  

Вопрос понимания научного статус IRT усугубился попытками внедрения положений этой теории в систему российского образования, как это ни странно,  не через науку, а через практику централизованного тестирования и ЕГЭ. А эта практика всегда держалась от педагогической науки как можно дальше. И нет пока признаков или попыток изменения этой нездоровой ситуации.

IRT точно не занимается вопросами понятийного аппарата педагогических измерений, содержания и формы тестовых заданий. И не может этим заниматься, потому что это формальная теория и это собственный предмет другой, ранее сформулированной теории - Педагогической Теории Измерений (ПТИ)[7], включающей главные вопросы обеспечения качества педагогических измерений. И поскольку в IRT нет никакого педагогического содержания, её правильнее рассматривать именно как формальную теорию, а не содержательную. Быть может, IRT когда-нибудь интегрируется в систему расширенного педагогического знания, но эффективно это может произойти, скорее всего, через объединение с с педагогической теорией измерений (ПТИ).  Последняя  намного ближе к педагогике, чем МТИ (IRT).

Педагогическая теория измерений является содержательно-педагогической, и только отчасти формальной педагогической теорией, имеющей своим предметом понятийный аппарат, форму и содержание тестовых заданий, вопросы разработки педагогических тестов, педагогической оценки уровня и структуры подготовленности испытуемых, проведения массового тестирования, сравнения и интерпретации результатов. Хотя объекты ПТИ и МТИ могут совпадать – а это тестовый процесс - каждая из теорий имеет свой предмет, свой понятийный аппарат, свои методы обоснования качества педагогических измерений. И ни одна теория не в состоянии заменить другую теорию.

Математическая теория измерений включает в себя также совокупность методов, позволяющих получить количественные оценки вероятности правильного ответа испытуемых на задания различного уровня трудности, уровня подготовленности испытуемых, меры трудности и различающей способности заданий, а также другие характеристики. Есть, правда, авторы, которые считают МТИ просто теорией шкалирования данных. Тогда её можно определить как теорию и методику логарифмического шкалирования уровней подготовленности испытуемых, а также уровней трудности и различающей способности тестовых заданий. Но это было бы очень узкое, если не сказать, ограниченное определение. Как и всякая развитая формальная теория,  IRT имеет свою собственную систему понятий, опирающихся, главным образом, на язык теории вероятностей, математики, вычислительных методов и статистики. В общем, на язык математики.

В фокусе исследования МТИ (IRT) – тестовое задание. Это теория, которая позволяет исследовать метрические свойства тестовых заданий, оценить их формальные свойства, пригодность для включения в тест, эффективность и качество тестовых заданий. Для этого используется вычисление стандартной ошибки измерения, значения хи-квадрат и определяется уровень достоверности получаемых выборочных статистик.

Вероятность правильного и неправильного ответа в МТИ рассматривается как функция от уровня подготовленности испытуемых и как функция от параметров заданий. В МТИ даётся решение и обратной задачи – определения меры правдоподобности оценок уровня подготовленности испытуемых, как функции от теоретической вероятности наблюдаемых эмпирических результатов тестирования и от тех же параметров заданий. Наиболее правдоподобные значения принимаются в качестве оценок истинных значений (параметров) подготовленности испытуемых.

Для того чтобы МТИ (IRT) проявлялась как эффективная теория, она должна быть эмпирически верифицируемой в своих многочисленных приложениях. Дело в том, что сама МТИ нередко используется в качестве методической гипотезы, в порядке апробации методов данной теории к результатам разрабатываемого или уже применяемого теста. Разумеется, речь может идти о гипотезе применимости МТИ для оценки тех или иных тестовых заданий.

Главная цель, сфера и главный смысл применения МТИ  – научное исследование качества тестовых заданий. По большому счёту, к работе с нетестовыми заданиями МТИ  недостаточно применима. Хотя такие попытки делались много раз, в том числе и для ЕГЭ[8]. Но надежды математиков создать с помощью МТИ тесты из нетестовых заданий являются тщетными. Применение МТИ для оценки качества нетестовых заданий порождает существенные системные противоречия в процессе измерения и особенно, при интерпретации данных. Тесты можно создать только из тестовых заданий. Обходных путей в этом деле нет!

Известно, что попытки решения проблем одной науки средствами другой науки в принципе обречены на неудачу. Наблюдаемое во всём мире, и особенно в России, увлечение исключительно математической стороной обоснования качества тестов, в ущерб педагогической стороне – явление не новое и не исключительное. На ситуацию выхолащивания представителями одной науки содержания другой науки в своё время обратил внимание Гегель. Попытки математиков задавать тон в философии он называл «варварским педантизмом или педантичным варварством, представленные во всей широте и со всей обстоятельностью, которые должны были привести к тому, чтобы геометрический метод лишился всякого доверия[9]».

Не случайно, например, в научной психологии, успешно применяющей математический аппарат уже примерно сто пятьдесят лет, было понято что математика не может претендовать на полное и действительное решение проблем, принадлежащих психологии и другим наукам[10]. Есть надежда, что признание IRT в качестве формальной теории поможет снять необоснованные претензии некоторых представителей математико-вычислительного направления в нынешнем практическом тестировании на решение чуть ли не всех содержательных и общих теоретических задач педагогических измерений. Это дорога в тупик, из которого выход только один - назад.

В нынешней практике педагогических измерений вопрос соотношения теорий становится одним из запутанных, и даже спекулятивных. В первой статье уже упоминались ранее дававшиеся эпитеты в адрес IRT как «научная и современная». На самом деле это не так. В педагогических измерениях требуется осмысленная концепция измерения, обоснование надёжности и валидности получаемых результатов, с точным указанием цели, для которой эти результаты адекватны[11]. Культурным педагогическое измерение с амбивалентными целями не бывает.

Истоки МТИ (IRT)

Гегель был прав, утверждая, что без истории нет теории. У каждой подлинно научной теории обычно бывает несколько источников и направлений развития. В случае с IRT часть таковых выделяется сравнительно легко. В зарубежной литературе можно насчитать десяток концептуальных источников и примерно два десятка фамилий авторов, внесших наибольший вклад в её развитие[12].

В этом разделе статьи внимание читателей обращается на семь источников.

Первый источник - это идея латентных (скрытых от непосредственного наблюдения) качеств личности. История возникновения таких идей прослеживается, начиная с трудов Платона. И хотя интересующее качество личности непосредственно не наблюдаемо и не измеряемо, оно проявляет себя в идее понятийных и эмпирических индикаторов. В тестовой технологии положительный или отрицательный ответ испытуемого на каждое задание теста рассматривается как индикатор наличия или отсутствия у него интересующего латентного качества.

Почти любое интересующее латентное качество личности имеет общее название «ability». Дословный перевод с английского как «способность» вызывает ошибки понимания. На русском языке применительно к педагогическим измерениям этому понятию лучше поставить в соответствие словосочетание «уровень подготовленности испытуемых». Примеры распространённости идеи латентных качеств можно найти также в поэзии[13] и в художественной литературе[14].

Второй источник становления IRT - идея построения графических образов отдельных заданий теста на основе эмпирических данных (A.Binet & N.Simon[15], 1916, М.W.Richardson[16], 1936).Эти авторы первыми реально увидели, как могут выглядеть графики различных заданий, построенные на идее подбора функции для эмпирически получаемых точек на плоскости.

Третий источник – это труды классика американской психометрики, Л.Гутмана. В его представлении задания должны располагаться на той же числовой оси, на которой определяется уровень подготовленности испытуемых, что стимулировало поиск такого методам шкалирования, который позволяет получить одну общую шкалу измерения, как для интересующего свойства заданий, так и испытуемых. Такую шкалу позже получил Г.Раш на основе разработанной им теории. Этим открылась возможность численно сравнивать ранее несравнимые свойства личности и различных вещей. Некоторые несравнимые ранее понятия стали теперь сравнимыми.

В тестовой технологии начала XX века большое распространение получило простое решающее правило: всякий испытуемый за правильное выполнение задание получал один балл, за неправильное выполнение – ноль. После чего каждое задание теста стало исполнять роль очередного порога (threshold) возрастающей трудности, которые испытуемый старался преодолеть в процессе тестирования: чем больше правильных ответов, тем лучше. Если располагать задания по принципу возрастающей трудности, то это способствовало появлению высокого числа баллов у хорошо подготовленных испытуемых. При ответах иногда возникали такие вектор-строки баллов испытуемых, в которых все нули следовали за всеми единицами. Такую вектор-строку можно назвать правильным профилем подготовленности испытуемого.

Редко у кого из испытуемых бывают правильные профили. Неправильные профили встречаются чаще, чем правильные. Те профили, где наблюдаются одна или несколько инверсий, логично назвать неправильными профилями подготовленности личности. Иногда неправильные ответы даётся на сравнительно лёгкие задания, а правильные – на трудные задания. Причин такого положения может быть несколько. Первая причина - это попытка угадывания правильного ответа в трудном задании, в случае использования заданий с выбором одного правильного ответа из числа предлагаемых на выбор.

При применении пяти ответов в каждом задании, из которых один правильный, а остальные неправильные, вероятность угадывания равна 1/5. Это означает, что примерно пятая часть ответов на все задания теста может быть угадана. Вторая причина - отсутствие у учащихся системных знаний. Эти и другие причины приводят к тому, что большая часть профилей оказываются неправильными. Здесь, и таким образом, в частности, проявляют себя ошибки педагогического измерения.

В теории Л.Гутмана вероятность успешного выполнения для тех испытуемых, кто в состоянии выполнить задание, равна единице. Для тех, кто не в состоянии, вероятность равна нулю. На рис.1 представлен графический образ задания среднего уровня трудности, которое безошибочно различает тех, кто знает, от тех, кто не знает. Это есть пример идеально функционирующего педагогического задания на своём уровне трудности.

Полезно выделить три важных условия получения идеальных заданий. Первое – содержание задания должно пониматься всеми испытуемыми, независимо от уровня их подготовленности. Иначе говоря, каждый должен понимать, о чём задание. Второе условие - форма заданий и инструкции к ней должны быть знакомыми. Третье условие идеальности задания – оно должно хорошо различать испытуемых ниже и выше точки трудности задания на оси абсцисс. Такие задания особенно привлекательны в случае, когда их много, и все они - непременно возрастающей трудности.

Тогда на числовой оси можно располагать десятки заданий возрастающей трудности, вследствие чего возникает эффект хорошего измерительного устройства, которое оценивает каждого испытуемого в зависимости от числа правильно выполненных заданий[17] теста.

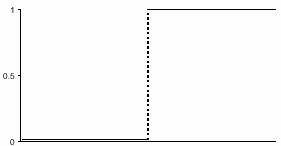
Рис.1. Графический образ задания, вытекающий из теории Гутмана.

            Результатом такого рода упорядочения испытуемых (по числу баллов) и расположения заданий по мере трудности получается своеобразная матрица тестовых результатов, элементы которой располагаются подобно прямоугольному треугольнику. На рис. 2 все правильные ответы располагаются в левом верхнем углу, все неправильные – в правом нижнем углу. Если при этом все профили испытуемых оказывались правильными, то такой вариант расположения результатов Л.Гутман называл шкалограммой.

Рис. 2. Пример т.н. шкалограммы

1	1	1
1	1	0
1	0	0
0	0	0

Позже требования Л.Гутмана к заданиям было названо детерминистической моделью измерения. У этой модели есть некоторые привлекательные свойства и одно, по меньшей мере, ограничение: все профили подготовленности должны быть правильными, что нереалистично. Правильность профиля педагогически можно истолковать так: испытуемый знает то, что знает (а это правильные ответы на сравнительно лёгкие задания) и не знает то, чего не знает – это неправильные ответы на трудные задания. Но для такого расположения испытуемых в матрице нужно было иметь и идеально упорядоченную, по мере возрастающей трудности, систему заданий.

Задания должны поддаваться правильному решению со стороны тех, кто подготовлен, и не поддаваться правильному решению для неподготовленных испытуемых. Каждое задание должно чётко различать испытуемых, на своём уровне трудности. Чем меньше ошибок, тем выше различающая способность задания. Но эту идеальную картинку отвергает противоречивая практика образования, которая редко у кого порождает стройную систему знаний. Суть этой главной проблемы образовательных систем и образовательных учреждений кратко и выразительно отметил великий русский поэт А.С.Пушкин: «Мы все учились понемногу, чему-нибудь, и как-нибудь!» Сам Гутман понимал идеализм своей теории, как понимал и её полезность для всякого, кто собирается создавать качественный тест. Нужно было искать более гибкие формы оценки качества заданий, допускающие возможности небольшого отклонения от шкалограммного идеала.

В попытках уйти от идеализма и жёсткого формализма своей теории у Л.Гутмана возникла идея перехода к вероятностной логике оценки качества заданий. В каждом задании вероятность правильного ответа испытуемых должна расти по мере повышения уровня подготовленности испытуемых. Так Л.Гутман пришёл к идее Marion Richardson строить для каждого задания теста график роста вероятности правильного ответа в зависимости от роста уровня подготовленности испытуемых. Чем выше подготовка, тем больше эмпирическая и теоретическая вероятность правильного ответа. Свой график Л.Гутман представлял в виде гладкой и непрерывно возрастающей функции. Такой график он назвал, вслед за П.Лазарсфельдом, trace line of the test item[18]. Пример графического образа задания представлен на рис.3. В психометрике и в теории педагогических измерений постепенно утвердилось другое название такого графика - Item Characteristic Curve.

Четвёртый источник развития IRT – результаты исследования D.N.Lawley, из Эдинбургского университета[19]. В 1943 году он опубликовал работу, показывающую, что некоторым понятиям статистической (классической) теории тестов[20] можно поставить в соответствие другие формальные показатели, вычислять их по новым формулам и тем самым делать оценки точнее. Вместо зависимых от выборки мер трудности заданий p и q  D.N.Lawley предложил считать параметр трудности задания (_j),   вследствие чего качество оценок улучшилось.

Рис. 3. Вероятность правильного ответа плавно возрастает по мере роста уровня подготовленности испытуемых.

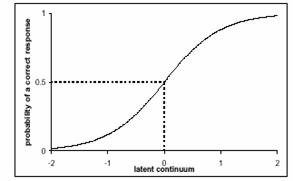
Переход к математическим функциям и их графикам имел недостатком потерю точек локализации мер трудности заданий на числовой оси, каковые имелись в теории Л.Гутмана. В поисках точек локализации авторы согласились считать в качестве показателя меры трудности заданий проекцию точки перегиба функции-графика задания на числовую ось. В однопараметрической модели именно в этой точке вероятность правильного ответа на задание равнялась ½. То есть этот вопрос был решён конвенционально.

Пятым источником IRT можно назвать исследования о возможности совместного шкалирования данных, имеющих разные исходные шкалы, в одной общей шкале:  уровня подготовленности испытуемых и параметров заданий[21]. Примерно так можно перевести на русский язык и идею, которая по-английски имеет название conjoint measurement (G.Rasch 1958). У истоков этой идеи стоял Л.Гутман, реализовали же её удачным образом Г.Раш и другие авторы[22].

Сам Г.Раш считал, что он совершил открытие в области психолого-педагогических измерений, но этот его образ мысли вызывал усмешку у большинства коллег и слушателей. У него на лекциях в США в аудитории оставался только один слушатель – Б.Райт. Спустя много лет Б. Райт сумел донести до учёных США, а затем и всего мира, действительный смысл открытия в области психолого-педагогических измерений, которое сделал Г.Раш.

Шестой источник развития IRT – работы F.M.Lord[23], A.Birnbaum[24] и многих их коллег, усилиями которых IRT приобрела современный облик. Главной заслугой Ф.Лорда можно считать разработку двухпараметрической модели педагогических и психологических измерений, методов оценки параметров заданий и участие в создании эффективной компьютерной программы «Logist», для одновременного расчёта параметров заданий и уровня подготовленности испытуемых методом максимального правдоподобия. У него хватило научной объективности оценить сравнительно большую практичность моделей А.Бирнбаума[25].

Ф. Лорд одним из первых исследовал соотношение между баллом испытуемого на латентной переменной величине, называемой «ability» ( в нашем случае, уровень подготовленности), наблюдаемым (исходным) тестовым баллом испытуемого и между истинным тестовым баллом испытуемого. Он установил, что все эти баллы должны иметь различное истолкование. Балл испытуемого на латентной переменной основан на идее абстрактно-истинного балла личности, независимого от теста, который применяется с целью педагогического измерения[26]. Наблюдаемый исходный тестовый балл испытуемого естественно зависит от применяемого теста (test dependent). Зависит от используемого теста и истинный (теоретический) тестовый балл, который определяется на основе получаемого при тестировании исходного тестового балла[27].

Публикация А.Бирнбаума была своеобразным ответом учёных США, безусловных лидеров в тестовых технологиях, на неожиданный научный прорыв датчанина Г.Раша, предложившего в конце пятидесятых годов, три свои модели психолого-педагогического измерения. Одна из моделей в США была замечена больше других и стала называться там однопараметрической моделью измерения. По логике текстов американских математиков-психометриков выходило, что работа Г.Раша – лишь это частный случай IRT, одна из трёх математических моделей измерения. Однако такая интерпретация не поддерживается рядом исследователей, равно как и автором этой статьи.

И, наконец, в качестве седьмого источника развития и внедрения IRT в практику хотелось бы упомянуть классическое пособие Ф. Бейкера[28]. По математической теории педагогических измерений (IRT) написано много хороших книг[29], но для начального изучения этой теории по краткости, систематичности, доступности и культуре изложения ничего лучшего пока нет. Поэтому начинать изучение IRT лучше всего с книги и компьютерных программ Ф.Бейкера.

Классификация основных понятий педагогических измерений

К настоящему времени научная лексика МТИ (IRT) насчитывает порядка тысячу терминов, помогающих проведению измерений во многих сферах и многих странах мира. Термином обычно называют слово или устойчивое словосочетание, которому приписывают определенное научное или специальное понятие. Процесс внедрения IRT в российскую практику педагогических измерений тормозится из-за того, что заметная часть терминов и понятийный аппарат нуждаются в системной разработке. С целью хотя бы некоторого упорядочения положения дел, в настоящей статье выделены четыре группы основных понятий:

Первую группу естественно образовать из понятий педагогики и теории педагогических измерений. Это:

- испытуемые (тестируемые);

- исходный тестовый балл испытуемых;

- педагогическое задание, задание в тестовой форме, тестовое задание;

- свойства испытуемых и заданий;

- тестовый процесс;

- процесс педагогических измерений и различных видов педагогического оценивания;

- педагогический тест.

Ко второй группе можно отнести основные математико-статистические понятия, распространенные преимущественно в статистической (классической) теории педагогических измерений[30]. Это:

- мера трудности задания  (item difficulty);

- тестовое задание и его статистические свойства;

- различающая способность задания (item discrimination);

- истинный тестовый балл испытуемого, определяемый в статистической (классической) теории тестов (True Test Score, обозначается T_i).

В классической теории есть два сильно различающихся варианта концептуализации истинного тестового балла. Первый называется specific true score. Это означает, что истинный тестовый балл можно получить как средний балл из всех параллельных вариантов теста. Второй вариант истинного тестового балла испытуемого называется generic true score, который можно получить как средний балл тестов, образованных выборками заданий из одной и той же генеральной совокупности заданий;

- одномерность (unidimensionality).

- надёжность и валидность тестовых результатов;

- стандартная ошибка измерения.

Некоторые российские авторы считают, что классическая статистическая теорию устарела. Из чего можно понять что после появления IRT она стала не нужной. Кроме этого заблуждения, наблюдается также случаи увлечения одним методом, одной теорией, например, только теорией Раша или Бирнбаума.  Но такого рода ограниченный подход приводит к ошибкам интерпретации данных, и в конечном итоге может превратиться в признак недостаточного епрофессионализма. При сравнении практической полезности теорий ведущие западные авторы считают классическую теорию обязательной, незаменимой[31]. И это абсолютно верное мнение.

Третью группу образуют понятия собственно IRT. Это:

- уровень подготовленности испытуемого, определяемый на латентной переменной величине (_i). Признание качества латентным означает, что в отличие от элементарных оценок и некоторых простых физических измерений процесс научно-педагогического измерения требует теоретизации. Куда входят проверка логической правильности имени измеряемого качества, определения ведущего понятия и выделяемого предмета, а также системы индикаторов, понятийных и эмпирических индикаторов, указывающих на наличие или отсутствие включаемых в понятие признаков интересующего качества[32];

-математические функции-модели измерения, определяющие вероятность правильного ответа на задание, в зависимости от уровня подготовленности испытуемых. Вероятность правильного ответа на задание зависит не только от уровня подготовленности испытуемого, но и от избранной модели измерения, каждая из которых может иметь один, два или три параметра[33].

- график функции, который в IRT ставится в соответствие каждому заданию. На английском языке эти функции называются Item Characteristic Curves. На русский язык вместо слова "график" их обычно переводят дословно и неблагозвучно: «характеристические кривые заданий» В данной статье такой перевод не поддерживается.

- показатель уровня трудности заданий в IRT (item difficulty parameter); обозначается символом _{j ,} где подстрочный символ j представляет номер задания (j = 1, 2….k), k – число заданий проектируемого теста.

- показатель уровня различающей[34] способности задания (item discrimination parameter) Различающей способностью задания называется его способность (свойство) дифференцировать испытуемых по уровню подготовленности[35]. Чем выше такая способность задания, тем лучше деление испытуемых на подготовленных и на не подготовленных. Уровень такой способности обозначается символом a_j.

- вероятность угадать ответ в случае, если все испытуемые не знают правильного ответа (item guessing parameter)[36]. Потенциальная возможность угадать правильный ответ обозначается символом c_j.

- истинный балл испытуемого i, определяемого по формуле D.N.Lawley. Обозначается двумя символами TS_i, с подстрочной буквой i, где i – номер испытуемого; i  принимает значения от 1 до N – где N – число испытуемых;

- информационная функция задания и теста;

- свойство локальной независимости ответов испытуемых одинакового уровня подготовленности на задания теста (Local Independence);

- принцип инвариантности (независимости) оценок уровня подготовленности испытуемых от уровня трудности заданий теста, а также независимости значений параметров заданий от уровня подготовленности тестируемых групп испытуемых;

- единица измерения, которая называется логит;

- шкалирование значений параметров испытуемых и параметров заданий в единой стандартизованной шкале натуральных логарифмов (test calibration).

- параметры функции.

- метод хи-квадрат для проверки соответствия заданий избранной модели измерения;

- уровень значимости выборочных статистик хи-квадрат.

К понятиям этой же группы можно отнести сотни понятий математики и вычислительных методов, (максимального правдоподобия, Байесовские и другие), используемые при статистическом моделировании, определении параметров испытуемых и заданий;

Четвёртую группу понятий целесообразно соотнести со специально-философскими, общенаучными и социально-политическими аспектами педагогических измерений. Это понятия:

- личность испытуемого;

- объективность педагогических измерений;

- качество педагогических измерений, критерии качества;

- понятийные и эмпирические индикаторы признаков понятия.

- справедливость оценивания, понятие «право испытуемых на объективную и справедливую оценку уровня их подготовленности». Часть приведённых понятий были уже определены в ряде предыдущих работ автора[37]. В этой статье основное внимание уделяется понятиям собственно IRT. Многие определения IRT были ранее сформулированы вне педагогического языка. В этой работе делается попытка дать определения основных понятий этой теории, согласованной с системой определений педагогических измерений, сформулированной ранее[38].

Задача педагогического измерения обычно формулируется как определение тестового балла и места испытуемого на числовой шкале уровня подготовленности. К этому добавляют и задачу определения параметров заданий. Что правильно с технической точки зрения. Но с педагогической точки зрения задача измерения стоит шире и глубже. Вопрос может ставиться об измерении интересующих свойств личности, а также содержательных и формальных свойств педагогических заданий. Поэтому самым первым следует признать понятие «личность испытуемого (тестируемого)»

Личность испытуемого

В нашей работе уже было определено, что в тестовом процессе испытуемые – это граждане, выражающие добровольное желание объективно определить уровень своей подготовленности и на этой основе решать вопросы своего социального и профессионального самоопределения. Если принцип добровольности не выполняется, то испытуемые превращаются в подопытных лиц, что нарушает их права, записанные в ст. 21 Конституции РФ. Главная разница между испытуемыми и подопытными лицами заключается именно в признаке добровольности участия в экспериментах (опытах)[39].

Все испытуемые имеют право на объективное измерение уровня их подготовленности, на своевременное получение объективной информации о собственных результатах, о результатах конкурирующих с ними других испытуемых, а также право на высокое качество измерений их знаний, умений, навыков и компетенций. Объективность возникает как следствие интеграции методов обоснования надежности и валидности тестовых результатов[40].

Объективность обеспечивается также такими моделями измерения, которые позволяют оценить уровень подготовленности испытуемого независимо от выборки заданий, доставшейся испытуемому в виде теста, и общей научной организацией тестового процесса. Объективность может быть обеспечена только совместной координированной деятельностью профессиональных, общественных и государственных органов управления образовательной деятельностью.

Уровень подготовленности личности

Второе основное понятие педагогической и математической теорий измерений - это уровень подготовленности личности. Оно уже рассматривалось в первой статье. Здесь остаётся только углубить, расширить и уточнить его.

Известны пять основных оценок результатов тестирования испытуемых, не считая производных. Для предупреждения неизбежной в таких случаях путаницы каждой оценке даётся в соответствие своя символика.

1. Первая оценка – это исходное эмпирическое значение тестового балла испытуемого, или короче, исходный тестовый балл испытуемого (Raw Test Score or Test Score). Обозначается символом X_i или Y_i  Исходный тестовый балл испытуемого получается элементарным сложением баллов, полученных каждым испытуемым по итогам выполнения всех заданий теста.

2. Вторая оценка – это истинный балл испытуемого. в варианте классической теории тестов (так она называлась раньше)[41]. Истинный балл в этом варианте классической теории обозначается символом T_i. Он определяется как математическое ожидание результатов по любому параллельному варианту теста, на которые мог бы, предположительно, ответить испытуемый. Значение T_i вычисляется как интервальная оценка, посредством построения доверительного интервала вокруг выборочного исходного тестового балла испытуемого i. Это делается по формуле T = X_i ± ts_{e ,}где t означает меру достоверности выборочных статистик по Стьюденту, а s_e – стандартная ошибка измерения. Для 5% уровня риска ошибки t принимается равным 1,96. Значение s_e определяется по формуле s_e = s_x, где s_x  равно стандартному отклонению исходных тестовых баллов испытуемых, а r_xx` означает надёжность результатов, определяемая коррелированием результатов испытуемых в двух параллельных вариантах теста.

3. Истинный тестовый балл испытуемого (True Score), по версии D.N.Lawely - это теоретически вычисляемый тестовый балл каждого испытуемого. Обозначается TS_i и вычисляется как сумма вероятностей правильных ответов испытуемого[42]. Для вычисления значений TS_i у каждого испытуемого он предложил формулу

                        TSi =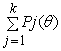

которая выражает смысл суммирования вероятностей правильного ответа каждого испытуемого на все задания теста, если известны параметры каждого задания.

4. Четвёртая оценка – это теоретически истинный тестовый балл испытуемого, значение параметра _i, не зависимого от выборки испытуемых и выборки заданий. Здесь уместно вновь обратиться к трактовке Ф.Лорда. Вопрос точности определения _i связан с уровнем дифференцированной стандартной ошибки измерения для каждого измеряемого уровня. А это, помимо прочего, всегда производное от объёма выборок. Позже будет отмечено, что качество оценок, получаемых при применении IRT, сильно зависит от объёма выборок. И это одно из существенных ограничений, накладываемых на её применение в практике.

5. В IRT уровень подготовленности испытуемых вычисляется на латентной переменной, как обратная задача по отношению к расчёту вероятности правильного ответа. Знание эмпирических вероятностей правильного ответа и знание параметров заданий позволяет получить оценки значения ˆ_i – уровней подготовленности испытуемых, где подстрочный символ i относится к испытуемому под номером i, и может принимать значения 1, 2, ....N.

Важно избавиться от распространённого мифа, что получаемые в единичном опыте измерения посредством IRT значения уровня подготовленности испытуемых ˆ_i – это и есть истинное значение параметра подготовленности испытуемого. На самом деле, это очередная оценка значения латентного параметра. Если дать испытуемому другой вариант теста, то нередко изменяется профиль баллов испытуемого, другой становится ошибка измерения, а значит, меняется и оценка ˆ_i.

Вообще, получаемые значения ˆ_i зависят от профиля тестовых баллов испытуемого, а он редко когда воспроизводится в точности у каждого испытуемого в параллельных вариантах теста. Таким образом, оценки значений ˆ_I в каждом случае измерения не равны точно истинным значениям уровня подготовленности испытуемых (параметра), а всего лишь являются тоже оценками, меняющимися от измерения к измерению. Мера вариации оценок ˆ_I  относительно параметра является стандартная ошибка измерения.

Математическая функция заданий и теста

Заданию, как педагогическому феномену, в нашем журнале уже были посвящены две большие статьи[43] автора. В этих статьях была поставлена и решена, в первом приближении, задача создания теории педагогических заданий.

В МТИ (IRT) творческим образом соединяются два феномена разных наук: задание - со стороны педагогической науки, и функции – со стороны математики. Всё началось с так называемой логистической функции, где аргументом является показатель степени

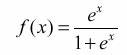
Поскольку в педагогических измерениях аргумент функции выражает не только число, но также и выражения, как буквенные, так и числовые, то принята другая, более удобная форма этой записи. Например, в функции вида

P_j() = {x_ij = 1 | _j }= exp ( - _j) / (1 + exp( - _j),

вместо х появилась разность значений двух параметров, ( - _j). Эта разность позволяет связать уровень подготовленности испытуемых (_i) с вероятностью правильного ответа на задание уровня трудности _j, где j - номер задания. Многие зарубежные авторы считают т.н. логистическую функцию самой существенным элементом IRT. График такой функции на английском языке имеет название Item Characteristic Curve. График функции – это линия на плоскости, отображающая уровни подготовленности испытуемых в значения вероятностей правильного ответа, на задание известного уровня трудности. В нашем случае график полезно рассматривать как образ тестового задания, представленный в системе прямоугольных координат на плоскости.

Хотя в практике обычно рассматривают один график, в IRT полезно принимать во внимание два графика. На рисунке 4 оба графика показывают значения вероятностей правильного ответа (красная линия) и неправильного ответа (чёрная линия), на одно и тоже задание. Значения вероятностей рассчитаны по однопараметрической модели, в зависимости от уровня подготовленности испытуемых. При изображении вероятности неправильного ответа по оси ординат откладывают значения Q(_i) , равные 1 - P(_i). Поскольку точки графика Q(_i) легко находятся из разности 1 - P(_i), то основное внимание исследователи обычно обращают на графики функции P(_i).

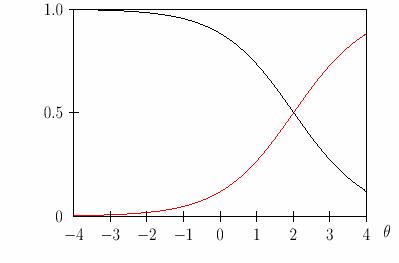
Рис.4. Графики зависимости вероятности правильного ответа (красная линия ) и неправильного ответа (черная линия) испытуемых от уровня подготовленности.

Часто бывает полезным построить график не отдельного задания, а теста в целом. На рис. 5 чёрные линии - это графики заданий, красная линия- график «теста», построенного всего лишь по пяти заданиям.

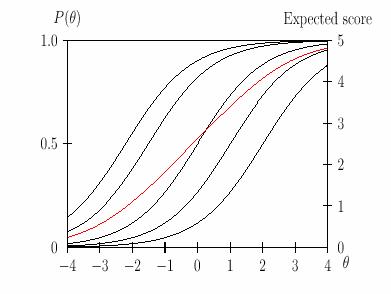
Рис. 5. Графики функций заданий и теста.

Когда математики говорят о функциях, то считается полезным указать на некоторые их свойства.

1.     Функция задания монотонная, возрастающая на оси . Чем выше значение испытуемого на латентной переменной, тем выше вероятность правильного ответа.

2.     Вероятность правильного ответа принимает значения между нулём и единицей.

3.     График этой функции - непрерывная линия.

 

Параметры функций

В математике параметрами функции обычно называются числа, которые в процессе вычисления значений зависимой переменной по значениям независимой переменной остаются постоянными. Простой пример функции Y = 3 + 2х где X и Y переменные величины, а коэффициенты 3 и 2 могут быть названы параметрами линейной функции. В данном случае параметры функции – это два числа, константы.

Функции бывают разными, их число может быть неограниченно. Для того чтобы число функций в IRT как-то минимизировать, было принято решение не фиксировать каждый раз в формуле значения параметров, а мыслить их в качестве переменных величин, так называемых переменных параметров функций. Так что в IRT слово «параметр» имеет другой смысл. Это качественно фиксированная, но переменная в количественном отношении латентная величина, различная для каждого задания и испытуемого. Параметры в IRT – это числа, которые используются в каждом вычислительном процессе. Их называют параметрами только потому, что они заранее неизвестны, за исключением одного. И их значения предстоит определить. Иначе говоря, надо определить значения параметров заданий и параметров испытуемых.

Обычно выделяется четыре параметра:

- уровень трудности задания (_j) , где j – номер задания;

- параметр крутизны графика функции задания. Обозначается a_j;

- уровень подготовленности испытуемых (_i), i – номер испытуемого;

- мера возможного угадывания правильного ответа на различные задания теста (с_j). Чем меньше число ответов к заданию, тем выше возможность угадывания правильного ответа.

Из этих четырёх только значение с_j определяется явно и может быть известно заранее, исходя из числа ответов к каждому заданию. Кроме того, в процессе поиска подходящего ответа проявляется не только удачливость, но и способности понимать, рассуждать, логически обосновывать своё решение. Вероятно поэтому Ф.Лорд называл с_j, параметром псевдоугадывания. Автор этой статьи склонен называть с_j псевдопараметром.

Есть ещё один, пятый параметр γ (читается гамма) представляет больше теоретический, чем практический интерес. Он плохо интерпретируем, но иногда бывает полезен. Формула с этим параметром представлена, в частности,  в диссертационной работе автора данной статьи[44].

Главным из трёх параметров заданий можно назвать параметр трудности. На рис.2 представлены проекции точки перегиба функции на ось абсцисс и на ось ординат. Поскольку в IRT уровень подготовленности испытуемых измеряется в одной и той же стандартной шкале логитов, как и уровень трудности заданий, проекция этой точки перегиба функции на ось абсцисс даёт меру трудности заданий. На рис. 6 красная стрелка показывает, что представленное, для примера, задание имеет уровень трудности плюс один логит. В теории Раша проекция точки перегиба функции на ось ординат в точности равно точке ½ на шкале вероятности правильного ответа. Там угадывание не допускается. Полезно эту же мысль выразить несколько иначе. Трудность задания определяется в такой точке графика, чтобы проекция этой точки на ось тета в точности совпадала с проекций на ось ординат, там, где вероятность правильного ответа на задание равнялось бы ½..

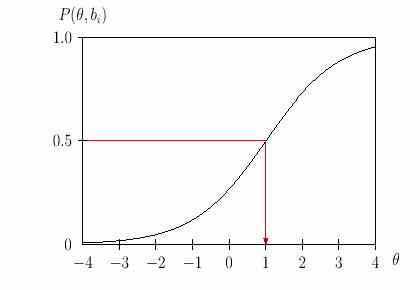
Рис.6. Определение значения параметра трудности задания.

Чем труднее задание, тем правее располагается его график. Точнее, проекция точки перегиба функции на ось абсцисс более трудного задания располагается правее. Этим объясняется другое английское название параметра трудности задания - location parameter. Графическая иллюстрация сравнительной меры трудности двух заданий представлена на рис. 7.

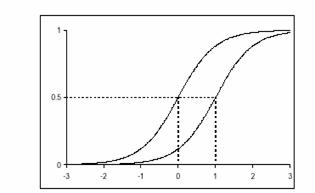
                        Рис.7. Различие графиков двух заданий по уровню трудности.

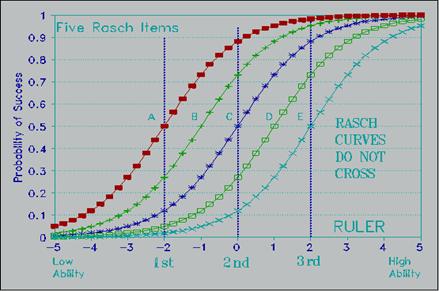
На рис.8 представлена система заданий возрастающей трудности. В Интернет можно найти такой пример графиков пяти заданий, с дидактической надписью на английском языке: «Rasch curves never cross», что означает, что в однопараметрической модели измерения графики заданий никогда не пересекаются. Это и есть одно из системных условий качественного педагогического измерения, присущих модели Г.Раша. При пересекающихся графиках заданий возрастает число ошибок измерения, а следовательно, ухудшается и качество теста. Это обстоятельство сильно снижает ценность двух и трёхпараметрических моделей IRT для создания теста как системы заданий возрастающей трудности, с непересекающимися графиками.

ость. 

Рис.8. Графики пяти заданий возрастающей трудности, с одинаковым

значением параметра крутизны.

Графический образ задания, меняется в зависимости от значений параметров a_j  и с_j. На рис. 9 задание, расположенное справа, труднее и имеет сравнительно большую различающую способность.

Влияние параметра а_j на графики двух заданий разного уровня трудности представлено на рис. 9. Этот параметр называется по-английски item discrimination parameter. Чем больше значения а_j, тем круче выглядит график задания. Соответственно, «крутыми» иногда называют и задания.

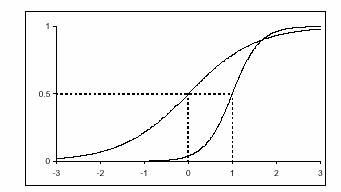
Рис.9. Второе задание труднее и имеет более высокий уровень

 различающей способности.

На рис.10 представлены задания одинакового, среднего уровня трудности, но имеющие неодинаковую меру различающей способности.

           

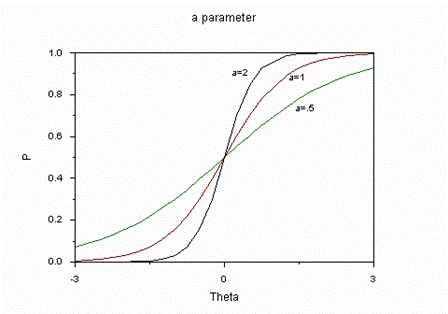
Рис.10. Изменение графиков заданий в зависимости от значений параметра а_j

Можно думать, что идея применения параметра а_j возникла из-за желания расшить возможности исследователей при подборе более подходящего графика для эмпирических точек. Сторонники IRT указывают на преимущества двухпараметрической модели перед однопараметрической, опираясь именно на этот тезис. Вопрос, однако, в том, что идея индивидуального подбора графиков для имеющихся данных находится в противоречии с идеей измерения по теории Раша: там, наоборот, данные должны соответствовать требованиям измеряемой модели. И это очень плодотворная идея с точки зрения создания теста как системы заданий равномерно возрастающей трудности. В этом пункте идеи Л.Гутмана и Г. Раша полностью совпали.

Влияние параметра с_j на изменение графика функции P(_i) представлено на рис. 11. Чисто теоретически идея применения параметра с_j в трёхпараметрической модели измерения кажется привлекательной. Появляется возможность делать коррекцию на угадывание правильного ответа в случае неподготовленности испытуемых. Испытуемые с низкой подготовкой имеют возможность угадать правильный ответ с вероятностью, зависящей от качества задания.  Абстрактно с_j может принимать значения от нуля до единицы. Практические пределы изменения значения с_j - от нуля до 0,5, в случае задания с двумя ответами, при качественном дистракторе. При некачественных дистракторах вероятность угадывания резко возрастает. Отсюда важная роль педагогического анализа не только содержания задания, но и содержания каждого ответа.

Г.Раш возражал против введения параметра с_j и использования его при тестировании испытуемых из-за вероятности угадывания правильного ответа. Вот почему для своего первого теста он просил коллег-психологов собрать данные с применением заданий открытой формы, где вероятность угадывания считается нулевой. Не одобрял он также использование в психолого-педагогических измерениях и переменных значений параметра а_j, справедливо полагая, что из заданий, имеющих графики различной крутизны, качественный тест не создать. Но к его мнению тогда не прислушивались.

Изменение значения параметра с_j влияет на крутизну графика задания. А это означает, что меняются значения параметров a_j и _{j .} В случае применения трёхпараметрической модели измерения мера трудности задания равна проекции на ось абсцисс точки графика    P() = с_j + (1 - с_j ) (.5) = (1 + с_j )/2.

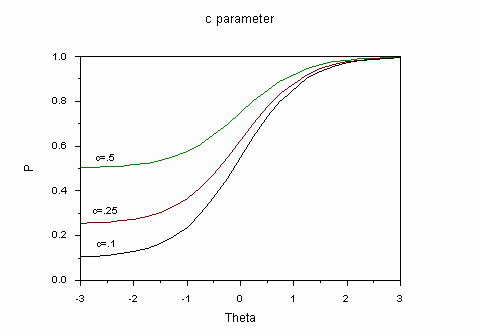
Рис.11. Влияние значения параметра с_j на изменение графика задания.

Нижним пределом значения функции становится не ноль, а значение с_j.

Не все функции IRT можно признать логистическими. Трёхпараметрическая модель измерения логистической не считается. Потому что не все свойства логистической функции на неё распространяются.

Свойство одномерности и локальной независимости

 Одномерность (unidimensionality) – это свойство отдельных заданий, включаемых в тест, и свойство теста как системы заданий. Суть этого свойства можно понимать так, что все задания в тесте измеряют преимущественно одно и тоже интересующее свойство личности. Если методами факторного (регрессионного) анализа элиминировать вариацию, определяемую данным свойством, то корреляции между заданиями должны становиться близкими нулю.

В МТИ (IRT) это свойство означает, что все задания подобраны так, что они имеют в своей основе только один латентный фактор. Хотя так бывает очень редко, ценность идеи одномерности от этого нисколько не снижается. Это тот идеал, к которому стремятся. Наличие этого свойства является решающим при оценке содержательной валидности тестовых результатов. Отсутствие одномерности, а следовательно, и валидности результатов теста, делает всю работу общественно бесполезной.

Старые западные тестологи сравнивали критерии валидности и надёжности тестовых результатов с определением времени по часам. Часы, имеющие ненадёжный ход, не могут показывать точное время. Но и надёжные (точно работающие) часы, будучи поставленными на неправильное время, тоже оказываются непригодными для ответа на главный вопрос – который час? Часы, имеющие ненадёжный ход, и поставленные неизвестно на какой час, полностью теряют возможность определить время. Так и тесты.

Если понятие «одномерность" относится к языку факторного анализа, то понятие локальная независимость относится к языку теории вероятности. Смысл этого термина «локальная независимость надо понимать так: Для испытуемых одного одинакового уровня  подготовленности (отсюда слово «локальная») вероятность правильного ответа на одно задание не зависит от вероятности правильного ответа на любое другое задание теста.

Эти два понятия связаны. Как показал F. Lord, если свойство одномерности заданий подтверждается, то проявляет себя и свойство локальной независимости заданий. (Lord, 1980).

Инвариантность значений параметров

В рамках классической теории педагогических измерений оценки уровня трудности заданий зависят от уровня подготовленности группы. Чем лучше подготовлена тестируемая группа, тем выше доля (процент) правильных ответов на задание, тем легче оказывается задание. И наоборот, в слабой группе испытуемых процент выполнения заданий заметно ниже. По этому поводу сложилась даже своеобразная терминология. Оценки трудности заданий, оцениваемые в рамках классической статистической теории, называют зависимыми от уровня подготовленности испытуемых каждой группы. По-английски такие оценки называют group-dependent.

В IRT значения параметров заданий принципиально (теоретически) независимы от уровня подготовленности групп тестируемых. Это очень полезное свойство вытекает из свойства функции задания. График рис.12 показывает распределение вероятностей правильных ответов в двух группах испытуемых – сильной, точки расположены в правой части графика, и слабой, точки которой расположены в левой части графика. Функция одна, параметры функции задания те же самые для обеих групп. Точки в окрестности графика указывают на пригодность данной функции задания для определения вероятности правильного ответа в любой из этих групп.

 

 

 

 

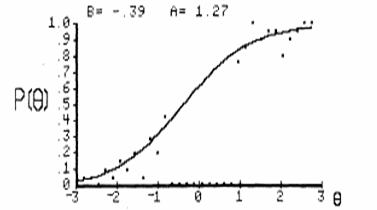
Рис.12. Свойство инвариантности параметров функции, независимых от уровня подготовленности испытуемых. Результаты слабой и сильной группы испытуемых располагаются вокруг соответствующих частей одного и того же графика функции задания.

Какую бы группу испытуемых мы ни взяли для определения параметров заданий, свойства функции заданий проявляются одинаковым образом. Это и есть свойство независимости параметров задания. На английском языке это называется the item invariance of an examinee’s ability. В данном случае инвариантность означает теоретическую независимость значений параметров заданий от уровня подготовленности испытуемых. Фактически некоторые флуктуации в зависимости от групп есть, но они не столь существенны, по сравнению с оценками трудности заданий, оцениваемыми в статистической теории тестов. Принцип остаётся в силе. Симметрично независимы и оценки параметра уровня подготовленности испытуемых от уровня трудности заданий. Иначе говоря, значение уровня подготовленности испытуемых можно определять в разных по уровню подготовленности группах. (the group invariance of an item’s parameters).

Таким образом, в IRT имеет место два вида независимых (инвариантных) значений: параметры заданий теоретически независимы от параметров подготовленности испытуемых, а параметры подготовленности испытуемых так же независимы от параметров заданий. Это и есть одно из главных открытий Г.Раша, на основе которого стала развиваться IRT. Измерения по теории Г.Раша и по IRT дали мощный толчок становлению западных образовательных технологий.

Информационная функция

Информационная функция и методы её расчёта являются важной частью научного аппарата IRT.

Это понятие и метод вычисления ввёл A.Birnbaum[45].

I() =

где I() означает информационную функцию от латентной переменной величины ;

- квадрат значения производной функции  в интересующей точке ;

 - вероятность неправильного ответа на то же задание j, в той же точке ;

k - число заданий теста.

Статус информационной функции трактуется по-разному. Одни авторы считают, что это понятие близко к понятию «надёжность тестовых результатов», другие – что оно имеет отношение и к валидности, третьи – к тому и другому. Автор данной статьи связывает эту функцию, кроме того, также с обоснованием эффективности теста и тестовых заданий[46] при проведении педагогических измерений. И нельзя сказать, что кто-то неправ, потому что информационная функция, как удачный статистический показатель, позволяет интерпретировать результаты с точки зрения всех перечисленных критериев.

Например, если вопрос касается надёжности тестовых результатов, то информационная функция показывает дифференцированную надёжность измерения каждого уровня подготовленности испытуемых. Не случайно в IRT полагают, что информационная функция указывает на локальную надёжность результатов (local reliability). При такой интерпретации информационной называют функцию, которая позволяет оценить меру точности измерения каждым отдельным заданием или тестом в целом.

Информационная функция свидетельствует о количестве информации, которое даёт каждое задание для измерения уровня подготовленности каждого испытуемого. Это количество зависит от значений близости оценок уровня подготовленности испытуемых и трудности задания. Чем ближе эти значения, тем более информативно (эффективно) задание для измерения уровня подготовленности испытуемых именно такого уровня подготовленности.

Для каждой модели измерения используется своя информационная функция. Для данных, представленных в дихотомической шкале (1/0) для модели Раша максимальное значение информационной функции равно 0,25. Это значение получается для заданий, имеющих среднюю меру трудности (p = q = 0,5). Тогда произведение pq = 0,25. В классической теории тестов этот показатель назывался дисперсией тестовых баллов по заданию, оцениваемому дихотомически. Доказательство максимума дисперсии, а равно и информационной функции, уже приводилось в наших работах. Если для данных модели Раша графики задания и информационной функции расположить на одной плоскости (рис.13) , то чёрная линия – это график задания, синяя линия- график информационной функции задания. На рис.13. красная линия указывает на проекции точки перегиба функции на ось абсцисс и ось ординат.

Рис. 13: Графики функции задания и информационной функции для модели Г.Раша.

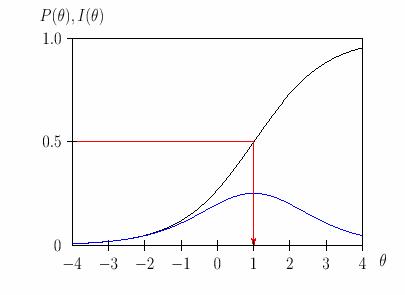
Максимум информации задание даёт для измерения уровня подготовленности испытуемых, у которых этот уровень в точности равен уровню трудности задания. Чем больше отличаются значения этих двух показателей, тем задание менее информативно с точки зрения эффективности измерения.

Поскольку информационная функция является функцией от латентной переменной, то смысл введения этой переменной требует краткого разъяснения. q представляет собой форму одномерной реализации идеи существования ненаблюдаемой переменной, детерминирующей, как фактор, результаты испытуемых на наблюдаемой переменной, получаемой элементарным сложением баллов. Результаты теста всегда содержат в себе ошибки измерения, затрудняющие оценку значения тестового балла на латентной переменной. Поскольку латентная переменная появляется в результате концептуализации, она всегда остается гипотетической переменной величиной, относительно которой с большей или меньшей точностью оцениваются истинные результаты испытуемых, получаемые на основе эмпирических данных.

Необходимую для оценки информативности производную функции , например, по теории G.Rasch получают, дифференцируя выражение

{ = 1|_j }= exp( - _j) / (1 + exp( - _j)

где = 1, если ответ любого испытуемого (i) на j-ое задание правильный;

- уровень знаний, латентная переменная;

_j  - уровень трудности j-го задания теста, измеряемой на латентном континууме.

Вероятность неправильного ответа на задание j, обозначаемая () и равная, как принято в теории вероятностей, 1 - P, выражается так:

 { = 0|_j } = 1 -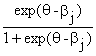

Элементарные преобразования правой части последней формулы посредством приведения разности к общему знаменателю 1+exp ( - _j) позволяют выразить ее в более удобном виде.

= 1/1+exp( - _j)

Симметрично, возникла и модель, описывающая вероятность правильного ответа студентов с уровнем знаний q _i на задания различного уровня трудности.

{ = 1|q} = exp( - _j) / 1 + exp( - _j)

Значения _i и _j могут быть аппроксимированы из матрицы эмпирических данных.

Производная функции получается посредством дифференцирования дроби

()` = () =

=

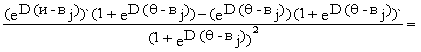
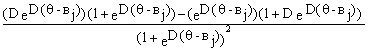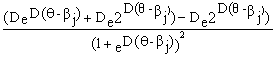
           После уничтожения подобных членов последнее выражение становится равным произведению двух дробей

и далее равняется произведению DPjQj.   Для варианта модели с добавлением константы D производная равна DPjQj.

Для модели G. Rasch, подставляя в формуле вместо равное ему выражение  и сокращая полученное выражение на , после выведения константы D за знак суммы получаем

I(q) =                              

Например, информационная функция теста, состоящего из k числа заданий, для модели G.Rasch, вычисляется посредством формулы

I (_i) = (P₁Q₁+P₂Q₂ +...+P_kQ_k)         

Поскольку значение константы заранее известно, то вопрос расчета информативности теста в избранной точке _i  сводится, таким образом, к нахождению суммы произведений вероятности правильного ответа на вероятность неправильного ответа в каждом задании. По справедливому утверждению F.M.Lord, информационная функция теста указывает на меру эффективности измерения на каждом уровне континуума знаний.

Интерпретация графика информационной функции столь же проста, сколь и эффективна для разработчика теста: чем больше значение I(_i), тем лучше тест измеряет. Максимум информации при измерении знаний испытуемых получается в той точке, где I(_i) принимает максимальное значение. В таких случаях можно говорить, что тест разработан для измерения знаний студентов с уровнем , где I(_i) принимает значение максимума. Там, где значение I(_i) минимально, можно определенно говорить о неэффективности теста для измерения знания у студентов с соответствующей подготовкой.

Использование информационной функции приводит, по сути, к оценке дифференцированной точности измерения, чего не было в статистической (классической) теории тестов. Там ошибка измерения принималась для всех испытуемых одинаковой. Если в качестве ошибок измерения s_e брать значения 1/I(_i) в точке _i, то ошибка измерения у разных испытуемых станет отличаться, в зависимости от полученного значения _i и от значений I().

Этот, казалось бы, на первый взгляд, математико-измерительный нюанс на самом деле отражает нечто большее, связанное с научным статусом тестов. Критики тестов интуитивно осознавали невозможность точного измерения знаний испытуемых различного уровня подготовленности, с помощью одного и того же теста. Это одна из причин того, что в практике стремились обычно создавать тесты, рассчитанные на измерение подготовленности испытуемых самого многочисленного, среднего уровня. Естественно, что при такой ориентации теста знания у сильных и слабых испытуемых измеряются с меньшей точностью.

Информационная функция в IRT считается не только для отдельного задания, но и для теста в целом. Для этого надо суммировать количество информации, даваемое в интересующей точке _i каждым заданием. Определение информационной функции теста для каждой интересующей точки оси тета даёт возможность целенаправленной разработки такого теста, который позволяет решать задачи, например, профотбора. Если надо отобрать половину лучших, то точность измерения повышают на уровне средней подготовленности, где и применяется данное решающее правило. В таких случаях в тест добавляют задания среднего уровня трудности. Но тогда очень плохо измеряется подготовка сильных и слабых испытуемых. Пример решения такого рода представлен на рис. 14.

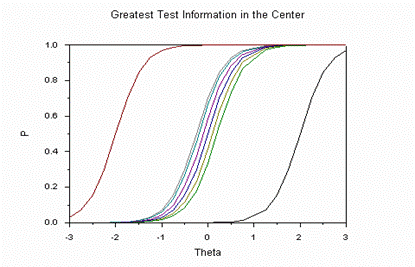
Рис.14. Измерение точнее для средне подготовленных испытуемых.

Если нужно, чтобы тест был эффективен на всём интересующем диапазоне подготовленности испытуемых, то задания теста стараются подобрать равномерно возрастающей трудности. Учебный пример такого рода равномерного подбора заданий «теста», состоящего всего из пяти заданий представлен на рис. 15.

Если нужно отобрать 10% лучших, то в тесте лёгкие задания не нужны. Их информационная ценность близка к нулю, в то время как включение трудных и очень трудных заданий при решении такой задачи повышает точность принимаемых кадровых решений и улучшает качество профотбора в целом.

Последним и очень важным в IRT понятием, которое получает здесь своё определение, это то, что по-английски называют test calibration. В текстах на русском языке это словосочетание переводится дословно как калибровка заданий или теста, что автору этой работы ни о чём хорошем не говорит.  Потому что этим словосочетанием операцией определяется не калибр теста, а совсем другое.

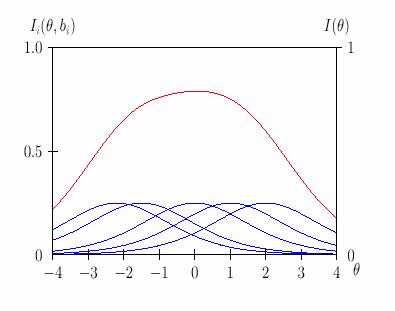
Рис.15. Информационные функции каждого задания (синий цвет) и «теста» в целом (красный цвет).

Ключ к интерпретации словосочетания test calibration лежит в правильном понимании сущности теста. Автору этой статьи уже не раз приходилось обращать внимание на то, что тест - это не просто набор или некое множество заданий, но также результаты тестирования, а также интерпретация результатов тестирования.

Таким образом, понятие «test calibration" на русском языке надо понимать как совместное шкалирование значений уровней подготовленности испытуемых, уровней трудности заданий и параметров крутизны заданий. Поскольку в модели Г.Раша фактор крутизны является константой, то остаётся шкалирование уровня подготовленности испытуемых и уровней трудности заданий.

Преимущества и ограничения RT

По сравнению с другими теориями измерений IRT имеет некоторые преимущества и ограничения. R.E.Schumacker[47] выделяет следующие преимущества IRT:

- оценки параметров заданий, определяемые с помощью IRT, не зависят от выборок испытуемых;

- оценки параметров испытуемых не зависят от уровня трудности теста в целом и от уровня трудности отдельных заданий;

- посредством IRT легче добиться соответствия уровня трудности заданий уровню подготовленности испытуемых, что повышает качество измерений;

- уровень подготовленности испытуемых и уровень трудности заданий определяется на одной и той же стандартной логарифмической шкале.

- надёжность тестовых результатов можно определить без применения параллельных вариантов теста.

Последнее из указанных преимуществ IRT открывает, казалось бы, возможность математического решения трудной педагогической задачи – создания параллельных вариантов теста. Однако история, теория и особенно практика педагогических измерений убеждают в необходимости разрабатывать параллельные варианты теста. Без чего невозможно качественно проводить массовое тестирование.

К перечисленным выше преимуществам иногда добавляют, что в IRT нет необходимости предполагать нормальность распределения тестовых результатов. Но для специалистов по педагогическим измерениям и это преимущество сомнительного толка. Так как отклонение исходных тестовых баллов от нормального распределения всегда связаны с нарушением баланса подбора заданий различного уровня трудности, а также несоответствием уровня трудности заданий уровню подготовленности испытуемых.

Кроме того, к положительным сторонам IRT относят философское свойство фальсифицируемости этой теории. То есть, всегда есть возможность убедиться в степени пригодности или непригодности любой применяемой модели для собранных данных. И в случае несоответствия искать другую модель. Но и это преимущество оборачивается недостатком, если смотреть на IRT с позиции теории измерения по Рашу. В теории Г.Раша заложена противоположная философия: данные должны подходить под используемую там математическую модель. И только тогда можно получить качественные измерения на интервальной шкале.

В числе ограничений этот же автор указывает, что применение IRT:

- основано на более строгих предположениях, чем применение вариантов классической статистической теории;

- требует математической подготовки, а потому эта теория плохо понимается педагогической общественностью и социумом, в котором эта теория применяется.

- требует больших выборок испытуемых для обоснования оценок параметров.

Критики IRT указывают также на поразительную корреляцию тестовых баллов испытуемых, полученных методами IRT (_i)и методами классической статистической теории измерений (X_i). Значения коэффициента корреляции между значениями _i и X_i на одном и том же множестве испытуемых равняются 0.99 и даже выше[48]. Тогда ставится вопрос – зачем применять IRT, если сравнительно простые методы приводят к столь сходным результатам[49]?

Простого ответа на этот вопрос нет. Здесь многое зависит от целей, критериев качества, уровня допустимых затрат и научности массовых исследований, программной оснащённости, от уровня некомпетентности и особенно от фактора Public Relation (PR). IRT хорошо использовать для экспертизы теста и тестовых заданий, для оценки соответствия уровня трудности задания уровню подготовленности испытуемых. Посредством IRT хорошо решаются локальные задачи определения ошибки измерения испытуемых определённого, определённого уровня подготовленности. IRT позволяет находить локальные коэффициенты надёжности тестовых результатов испытуемых интересующего уровня подготовленности на основе значений информационной функции.  

Вообще, IRT – это теория,  используемая для научного анализа качества тестовых заданий и теста в целом. Массовое применение этой теории для разработки тестов требует специального обучения тех, кто уже владеет началами педагогической и статистической теорий  измерений. Широкомасштабное применение IRT, задуманное из благих целей, при недостатке образования может привести к профанации и этой теории. Так что и в этом деле требуется определённая сдержанность и культура[50].   Что касается обобщённых или интегральных характеристик тестовых результатов, таких как надёжность и валидность тестовых результатов, то здесь значительная роль отводится классической статистической теории измерений. IRT бесполезна для решения задач педагогической теории измерений: при разработке тестовых форм, содержания тестовых заданий и теста. Потому что, как уже отмечалось, IRT – формальная педагогическая теория.

Успех в применении IRT для решения задач образовательной практики и педагогической науки возможен только при интеграции её возможностей с теоретическим и методическим арсеналом других  теорий педагогических измерений.